Recurrent neural network models for working memory of continuous variables: activity manifolds, connectivity patterns, and dynamic codes
Paper and Code
Nov 01, 2021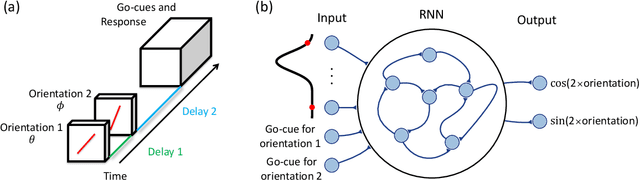
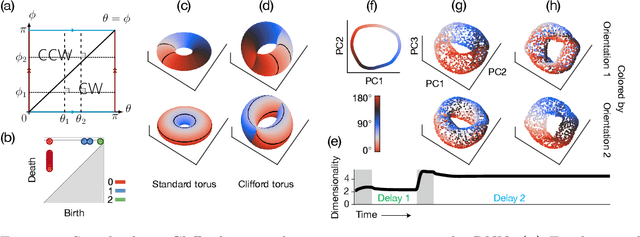
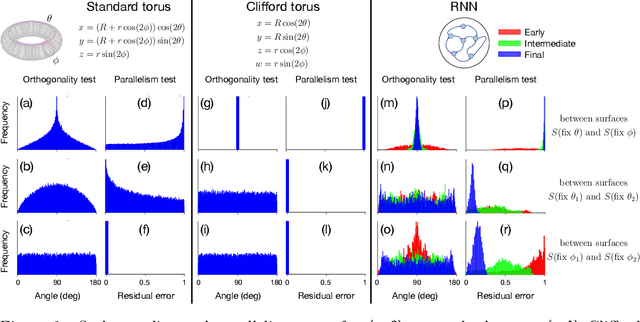
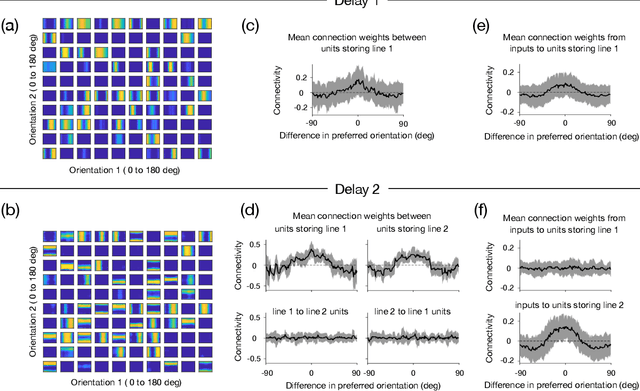
Many daily activities and psychophysical experiments involve keeping multiple items in working memory. When items take continuous values (e.g., orientation, contrast, length, loudness) they must be stored in a continuous structure of appropriate dimensions. We investigate how this structure is represented in neural circuits by training recurrent networks to report two previously shown stimulus orientations. We find the activity manifold for the two orientations resembles a Clifford torus. Although a Clifford and standard torus (the surface of a donut) are topologically equivalent, they have important functional differences. A Clifford torus treats the two orientations equally and keeps them in orthogonal subspaces, as demanded by the task, whereas a standard torus does not. We find and characterize the connectivity patterns that support the Clifford torus. Moreover, in addition to attractors that store information via persistent activity, our networks also use a dynamic code where units change their tuning to prevent new sensory input from overwriting the previously stored one. We argue that such dynamic codes are generally required whenever multiple inputs enter a memory system via shared connections. Finally, we apply our framework to a human psychophysics experiment in which subjects reported two remembered orientations. By varying the training conditions of the RNNs, we test and support the hypothesis that human behavior is a product of both neural noise and reliance on the more stable and behaviorally relevant memory of the ordinal relationship between the two orientations. This suggests that suitable inductive biases in RNNs are important for uncovering how the human brain implements working memory. Together, these results offer an understanding of the neural computations underlying a class of visual decoding tasks, bridging the scales from human behavior to synaptic connectivity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge