Recovery of Linear Components: Reduced Complexity Autoencoder Designs
Paper and Code
Dec 14, 2020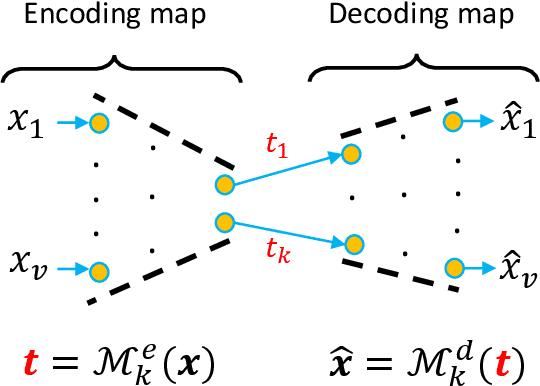
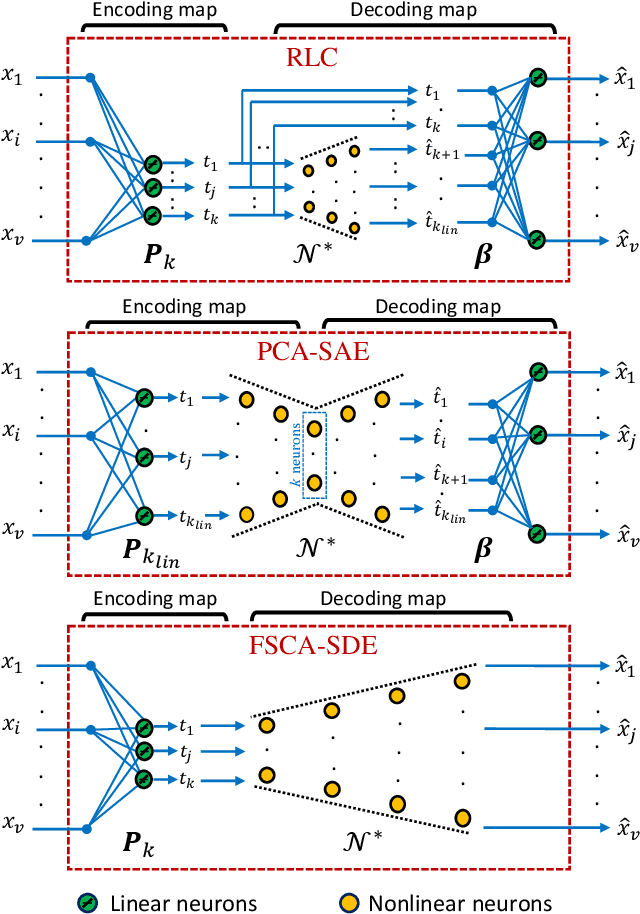
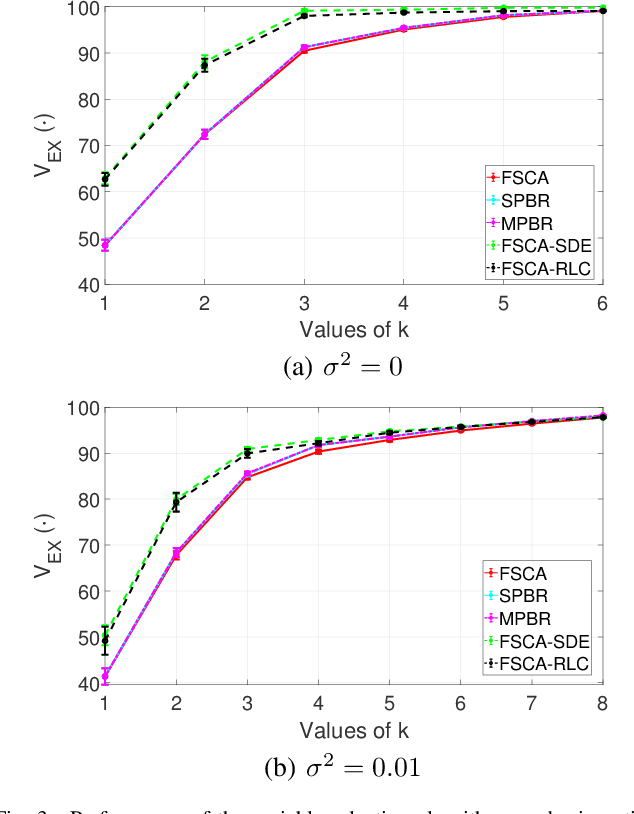

Reducing dimensionality is a key preprocessing step in many data analysis applications to address the negative effects of the curse of dimensionality and collinearity on model performance and computational complexity, to denoise the data or to reduce storage requirements. Moreover, in many applications it is desirable to reduce the input dimensions by choosing a subset of variables that best represents the entire set without any a priori information available. Unsupervised variable selection techniques provide a solution to this second problem. An autoencoder, if properly regularized, can solve both unsupervised dimensionality reduction and variable selection, but the training of large neural networks can be prohibitive in time sensitive applications. We present an approach called Recovery of Linear Components (RLC), which serves as a middle ground between linear and non-linear dimensionality reduction techniques, reducing autoencoder training times while enhancing performance over purely linear techniques. With the aid of synthetic and real world case studies, we show that the RLC, when compared with an autoencoder of similar complexity, shows higher accuracy, similar robustness to overfitting, and faster training times. Additionally, at the cost of a relatively small increase in computational complexity, RLC is shown to outperform the current state-of-the-art for a semiconductor manufacturing wafer measurement site optimization application.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge