Recovering Linear Causal Models with Latent Variables via Cholesky Factorization of Covariance Matrix
Paper and Code
Nov 01, 2023
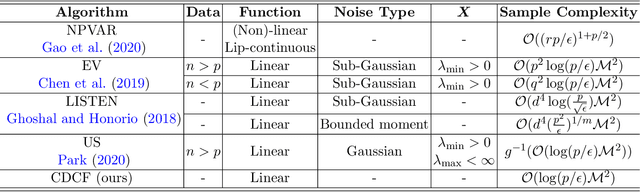
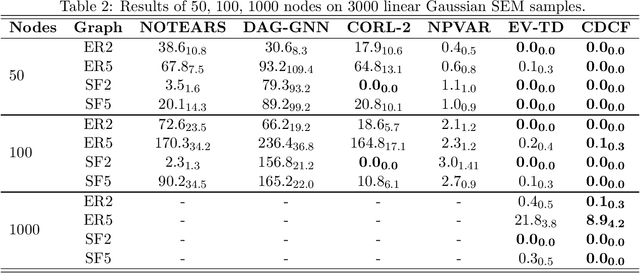
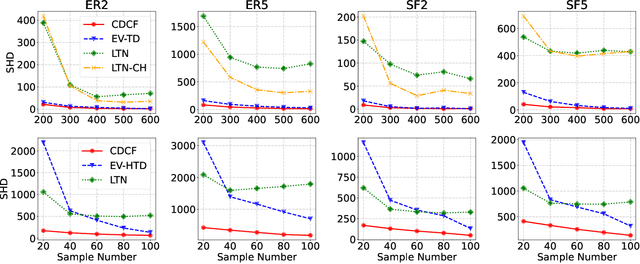
Discovering the causal relationship via recovering the directed acyclic graph (DAG) structure from the observed data is a well-known challenging combinatorial problem. When there are latent variables, the problem becomes even more difficult. In this paper, we first propose a DAG structure recovering algorithm, which is based on the Cholesky factorization of the covariance matrix of the observed data. The algorithm is fast and easy to implement and has theoretical grantees for exact recovery. On synthetic and real-world datasets, the algorithm is significantly faster than previous methods and achieves the state-of-the-art performance. Furthermore, under the equal error variances assumption, we incorporate an optimization procedure into the Cholesky factorization based algorithm to handle the DAG recovering problem with latent variables. Numerical simulations show that the modified "Cholesky + optimization" algorithm is able to recover the ground truth graph in most cases and outperforms existing algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge