Reconstructing Training Data with Informed Adversaries
Paper and Code
Jan 13, 2022
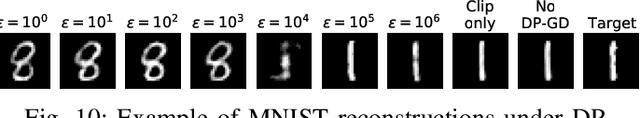
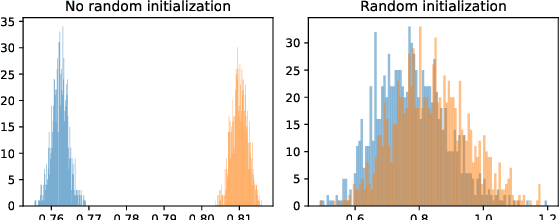
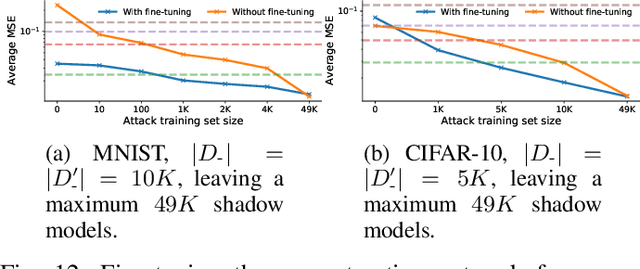
Given access to a machine learning model, can an adversary reconstruct the model's training data? This work studies this question from the lens of a powerful informed adversary who knows all the training data points except one. By instantiating concrete attacks, we show it is feasible to reconstruct the remaining data point in this stringent threat model. For convex models (e.g. logistic regression), reconstruction attacks are simple and can be derived in closed-form. For more general models (e.g. neural networks), we propose an attack strategy based on training a reconstructor network that receives as input the weights of the model under attack and produces as output the target data point. We demonstrate the effectiveness of our attack on image classifiers trained on MNIST and CIFAR-10, and systematically investigate which factors of standard machine learning pipelines affect reconstruction success. Finally, we theoretically investigate what amount of differential privacy suffices to mitigate reconstruction attacks by informed adversaries. Our work provides an effective reconstruction attack that model developers can use to assess memorization of individual points in general settings beyond those considered in previous works (e.g. generative language models or access to training gradients); it shows that standard models have the capacity to store enough information to enable high-fidelity reconstruction of training data points; and it demonstrates that differential privacy can successfully mitigate such attacks in a parameter regime where utility degradation is minimal.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge