Reconfiguration of 3D Crystalline Robots Using O(log n) Parallel Moves
Paper and Code
Aug 17, 2009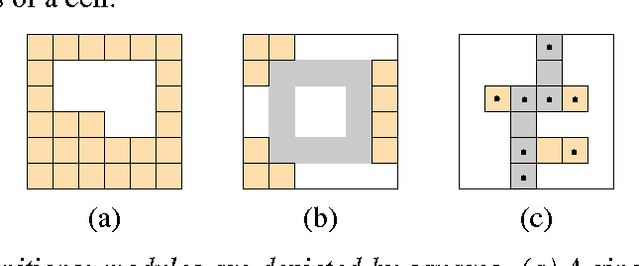
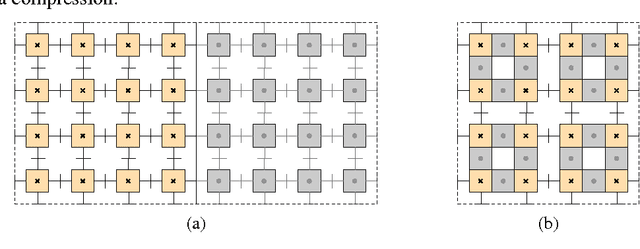
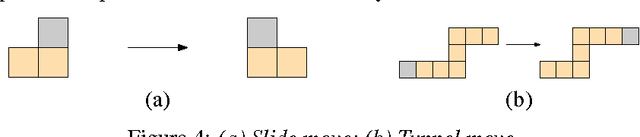
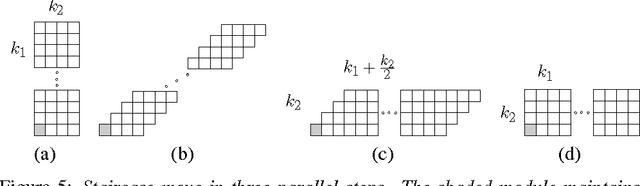
We consider the theoretical model of Crystalline robots, which have been introduced and prototyped by the robotics community. These robots consist of independently manipulable unit-square atoms that can extend/contract arms on each side and attach/detach from neighbors. These operations suffice to reconfigure between any two given (connected) shapes. The worst-case number of sequential moves required to transform one connected configuration to another is known to be Theta(n). However, in principle, atoms can all move simultaneously. We develop a parallel algorithm for reconfiguration that runs in only O(log n) parallel steps, although the total number of operations increases slightly to Theta(nlogn). The result is the first (theoretically) almost-instantaneous universally reconfigurable robot built from simple units.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge