Reciprocal Multi-Robot Collision Avoidance with Asymmetric State Uncertainty
Paper and Code
Jul 22, 2021

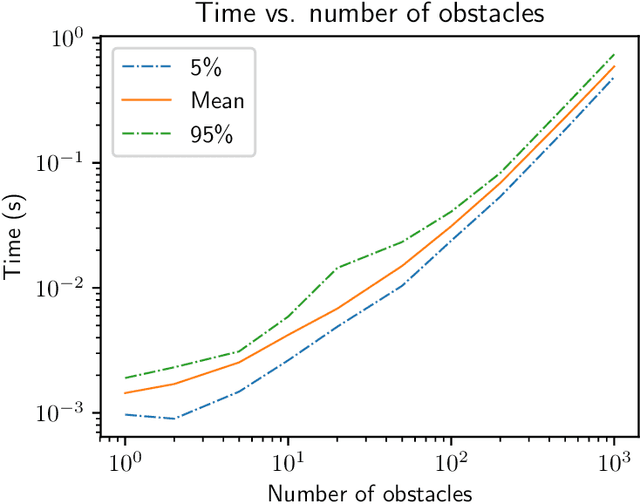
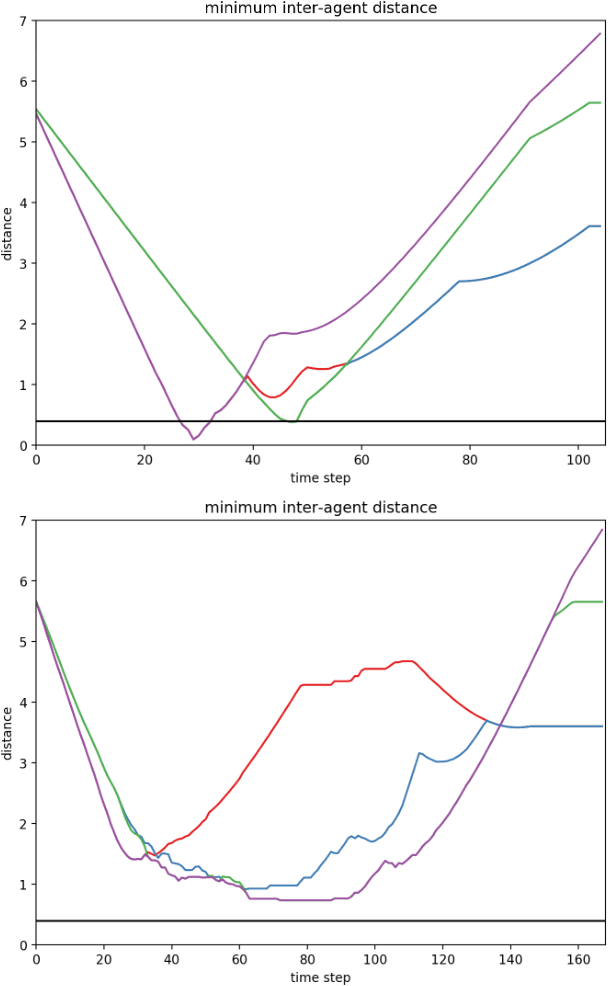
We present a general decentralized formulation for a large class of collision avoidance methods and show that all collision avoidance methods of this form are guaranteed to be collision free. This class includes several existing algorithms in the literature as special cases. We then present a particular instance of this collision avoidance method, CARP (Collision Avoidance by Reciprocal Projections), that is effective even when the estimates of other agents' positions and velocities are noisy. The method's main computational step involves the solution of a small convex optimization problem, which can be quickly solved in practice, even on embedded platforms, making it practical to use on computationally-constrained robots such as quadrotors. This method can be extended to find smooth polynomial trajectories for higher dynamic systems such at quadrotors. We demonstrate this algorithm's performance in simulations and on a team of physical quadrotors. Our method finds optimal projections in a median time of 17.12ms for 285 instances of 100 randomly generated obstacles, and produces safe polynomial trajectories at over 60hz on-board quadrotors. Our paper is accompanied by an open source Julia implementation and ROS package.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge