Receptive Field Size Optimization with Continuous Time Pooling
Paper and Code
Nov 06, 2020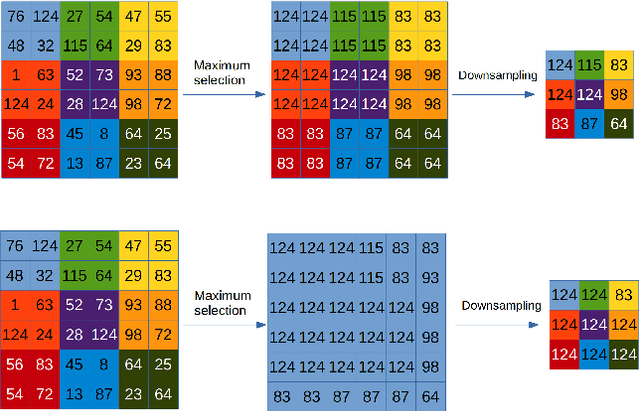
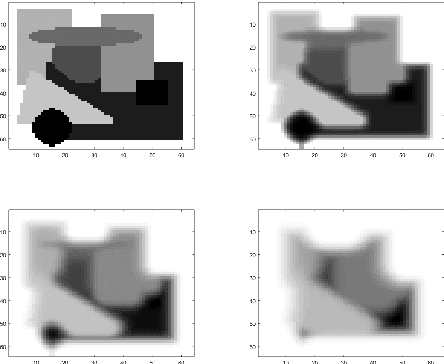
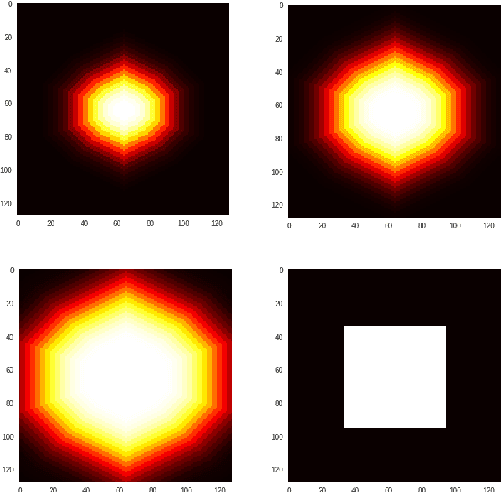
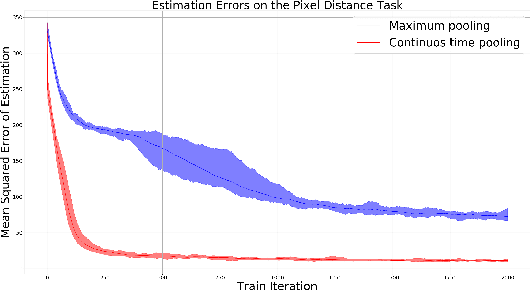
The pooling operation is a cornerstone element of convolutional neural networks. These elements generate receptive fields for neurons, in which local perturbations should have minimal effect on the output activations, increasing robustness and invariance of the network. In this paper we will present an altered version of the most commonly applied method, maximum pooling, where pooling in theory is substituted by a continuous time differential equation, which generates a location sensitive pooling operation, more similar to biological receptive fields. We will present how this continuous method can be approximated numerically using discrete operations which fit ideally on a GPU. In our approach the kernel size is substituted by diffusion strength which is a continuous valued parameter, this way it can be optimized by gradient descent algorithms. We will evaluate the effect of continuous pooling on accuracy and computational need using commonly applied network architectures and datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge