Randomly initialized EM algorithm for two-component Gaussian mixture achieves near optimality in $O(\sqrt{n})$ iterations
Paper and Code
Aug 28, 2019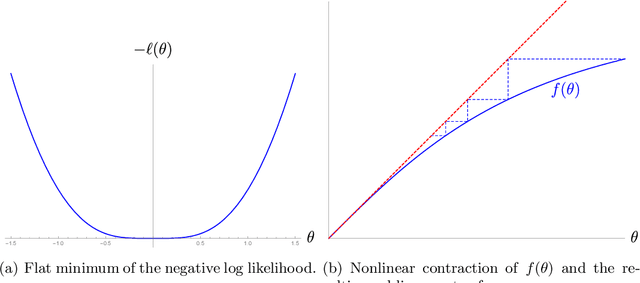
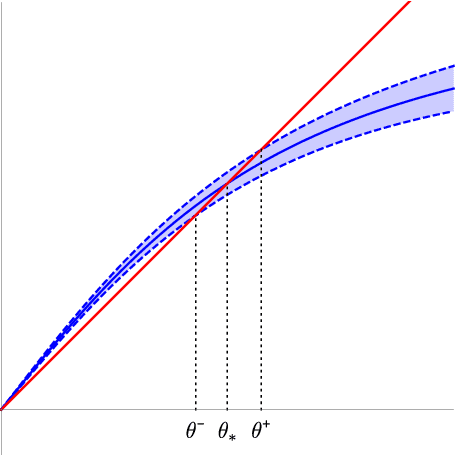
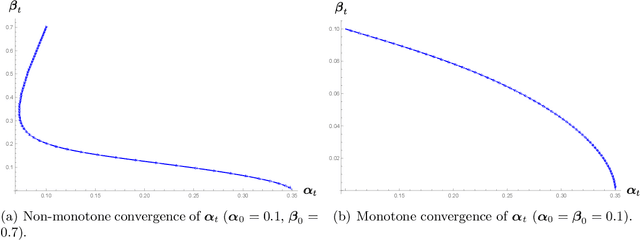
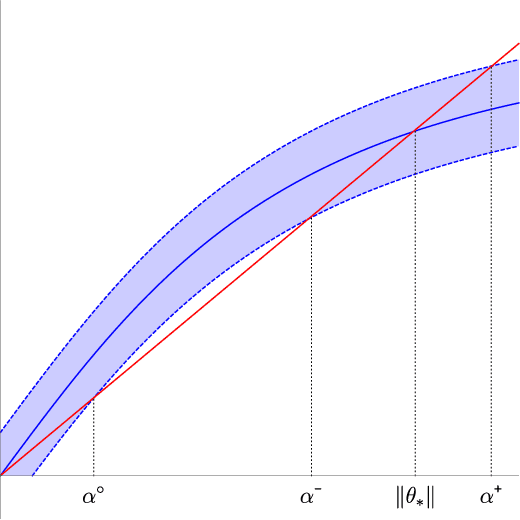
We analyze the classical EM algorithm for parameter estimation in the symmetric two-component Gaussian mixtures in $d$ dimensions. We show that, even in the absence of any separation between components, provided that the sample size satisfies $n=\Omega(d \log^3 d)$, the randomly initialized EM algorithm converges to an estimate in at most $O(\sqrt{n})$ iterations with high probability, which is at most $O((\frac{d \log^3 n}{n})^{1/4})$ in Euclidean distance from the true parameter and within logarithmic factors of the minimax rate of $(\frac{d}{n})^{1/4}$. Both the nonparametric statistical rate and the sublinear convergence rate are direct consequences of the zero Fisher information in the worst case. Refined pointwise guarantees beyond worst-case analysis and convergence to the MLE are also shown under mild conditions. This improves the previous result of Balakrishnan et al \cite{BWY17} which requires strong conditions on both the separation of the components and the quality of the initialization, and that of Daskalakis et al \cite{DTZ17} which requires sample splitting and restarting the EM iteration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge