Random ReLU Features: Universality, Approximation, and Composition
Paper and Code
Oct 10, 2018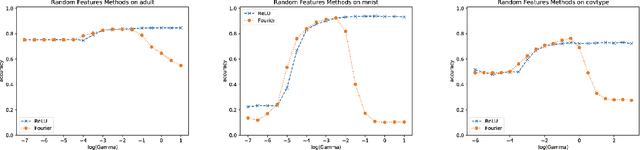
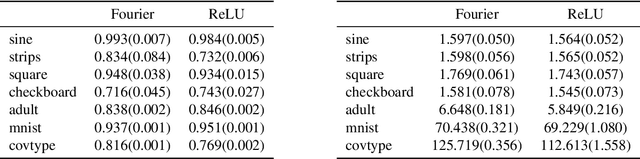
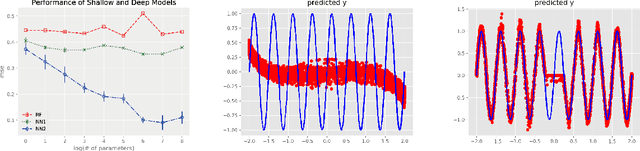
We propose random ReLU features models in this work. Its motivation is rooted in both kernel methods and neural networks. We prove the universality and generalization performance of random ReLU features. Parallel to Barron's theorem, we consider the ReLU feature class, extended from the reproducing kernel Hilbert space of random ReLU features, and prove a strong quantitative approximation theorem, where both inner weights and outer weights of the the neural network with ReLU nodes as an approximator are bounded by constants. We also prove a similar approximation theorem for composition of functions in ReLU feature class by multi-layer ReLU networks. Separation theorem between ReLU feature class and their composition is proved as a consequence of separation between shallow and deep networks. These results reveal nice properties of ReLU nodes from the view of approximation theory, providing support for regularization on weights of ReLU networks and for the use of random ReLU features in practice. Our experiments confirm that the performance of random ReLU features is comparable with random Fourier features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge