Random Intersection Chains
Paper and Code
Apr 10, 2021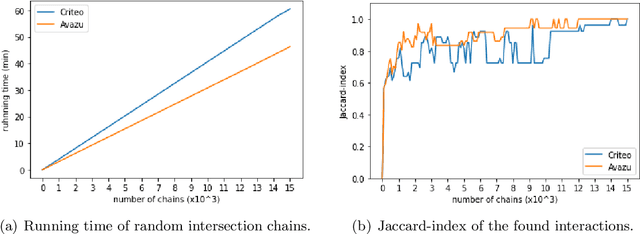
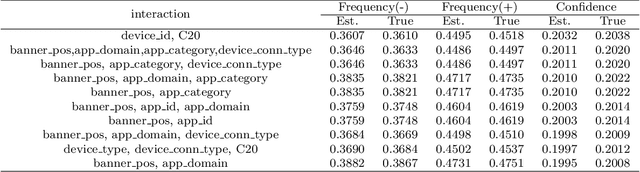
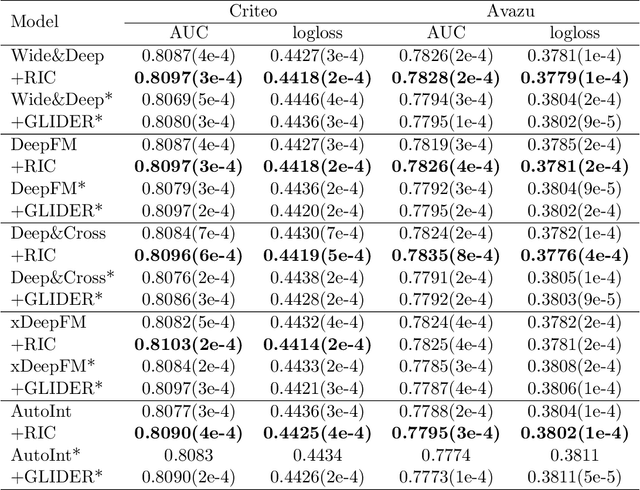
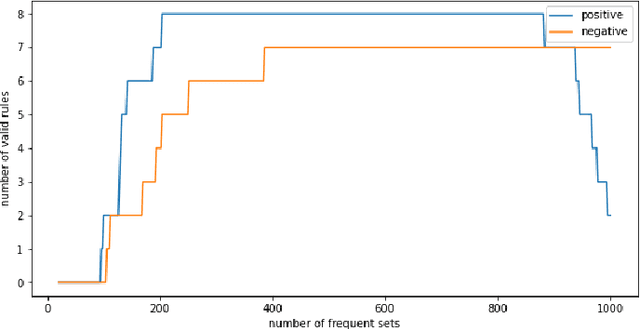
Interactions between several features sometimes play an important role in prediction tasks. But taking all the interactions into consideration will lead to an extremely heavy computational burden. For categorical features, the situation is more complicated since the input will be extremely high-dimensional and sparse if one-hot encoding is applied. Inspired by association rule mining, we propose a method that selects interactions of categorical features, called Random Intersection Chains. It uses random intersections to detect frequent patterns, then selects the most meaningful ones among them. At first a number of chains are generated, in which each node is the intersection of the previous node and a random chosen observation. The frequency of patterns in the tail nodes is estimated by maximum likelihood estimation, then the patterns with largest estimated frequency are selected. After that, their confidence is calculated by Bayes' theorem. The most confident patterns are finally returned by Random Intersection Chains. We show that if the number and length of chains are appropriately chosen, the patterns in the tail nodes are indeed the most frequent ones in the data set. We analyze the computation complexity of the proposed algorithm and prove the convergence of the estimators. The results of a series of experiments verify the efficiency and effectiveness of the algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge