RAN-GNNs: breaking the capacity limits of graph neural networks
Paper and Code
Mar 29, 2021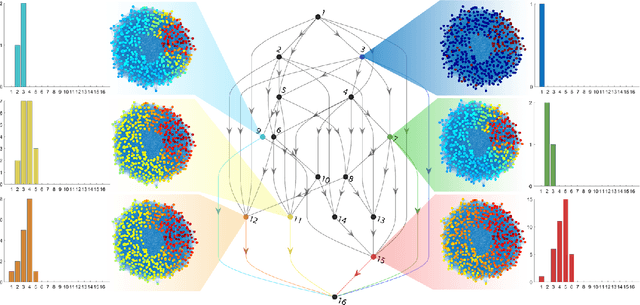
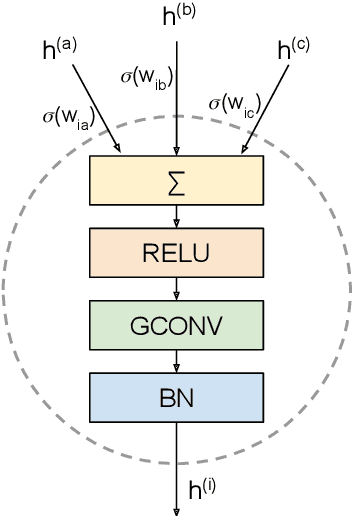
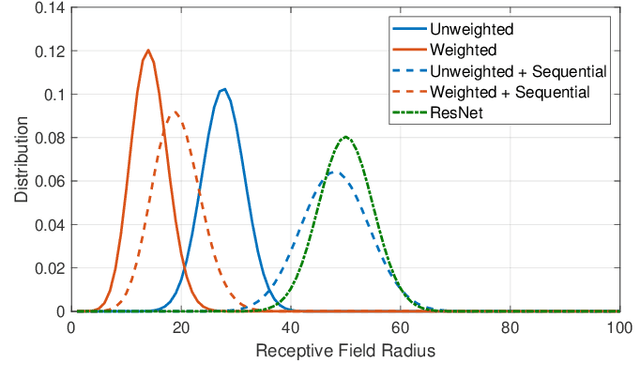
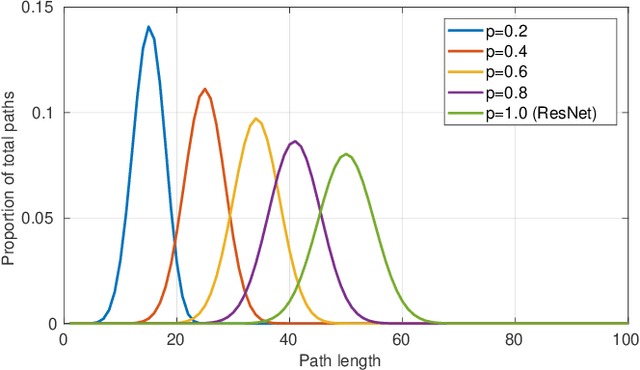
Graph neural networks have become a staple in problems addressing learning and analysis of data defined over graphs. However, several results suggest an inherent difficulty in extracting better performance by increasing the number of layers. Recent works attribute this to a phenomenon peculiar to the extraction of node features in graph-based tasks, i.e., the need to consider multiple neighborhood sizes at the same time and adaptively tune them. In this paper, we investigate the recently proposed randomly wired architectures in the context of graph neural networks. Instead of building deeper networks by stacking many layers, we prove that employing a randomly-wired architecture can be a more effective way to increase the capacity of the network and obtain richer representations. We show that such architectures behave like an ensemble of paths, which are able to merge contributions from receptive fields of varied size. Moreover, these receptive fields can also be modulated to be wider or narrower through the trainable weights over the paths. We also provide extensive experimental evidence of the superior performance of randomly wired architectures over multiple tasks and four graph convolution definitions, using recent benchmarking frameworks that addresses the reliability of previous testing methodologies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge