Query Answering over Contextualized RDF/OWL Knowledge with Forall-Existential Bridge Rules: Decidable Finite Extension Classes (Post Print)
Paper and Code
Dec 12, 2015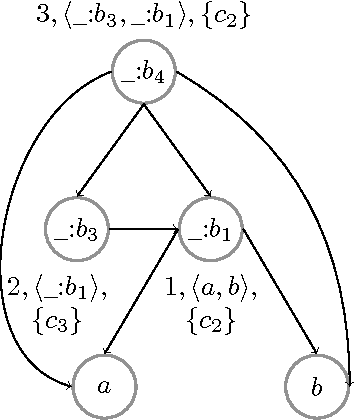
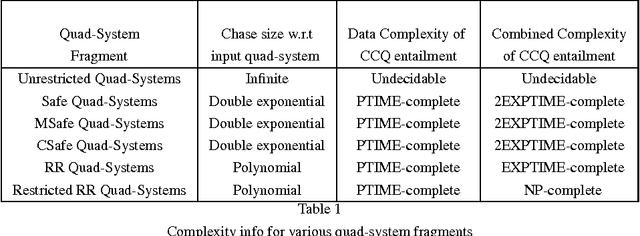
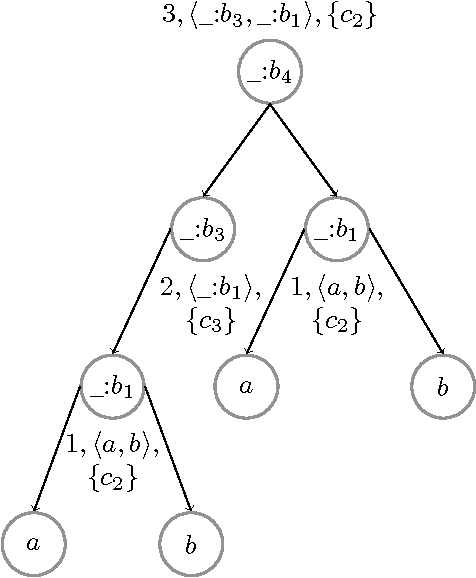
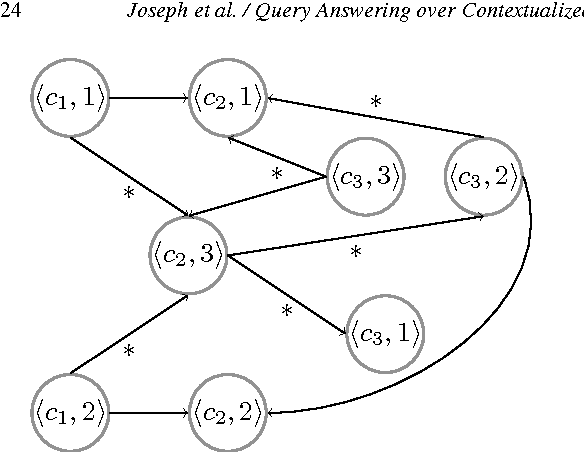
The proliferation of contextualized knowledge in the Semantic Web (SW) has led to the popularity of knowledge formats such as \emph{quads} in the SW community. A quad is an extension of an RDF triple with contextual information of the triple. In this paper, we study the problem of query answering over quads augmented with forall-existential bridge rules that enable interoperability of reasoning between triples in various contexts. We call a set of quads together with such expressive bridge rules, a quad-system. Query answering over quad-systems is undecidable, in general. We derive decidable classes of quad-systems, for which query answering can be done using forward chaining. Sound, complete and terminating procedures, which are adaptations of the well known chase algorithm, are provided for these classes for deciding query entailment. Safe, msafe, and csafe class of quad-systems restrict the structure of blank nodes generated during the chase computation process to be directed acyclic graphs (DAGs) of bounded depth. RR and restricted RR classes do not allow the generation of blank nodes during the chase computation process. Both data and combined complexity of query entailment has been established for the classes derived. We further show that quad-systems are equivalent to forall-existential rules whose predicates are restricted to ternary arity, modulo polynomial time translations. We subsequently show that the technique of safety, strictly subsumes in expressivity, some of the well known and expressive techniques, such as joint acyclicity and model faithful acyclicity, used for decidability guarantees in the realm of forall-existential rules.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge