Quaternion Graph Neural Networks

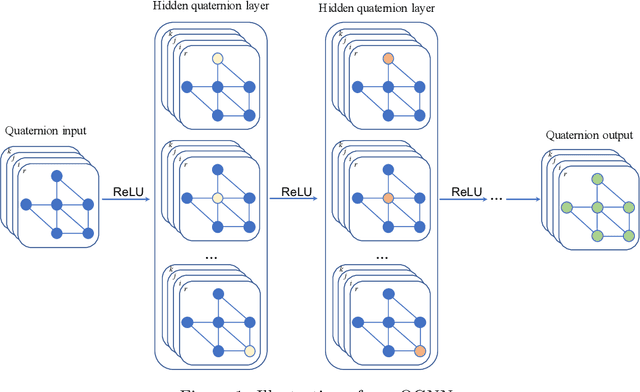
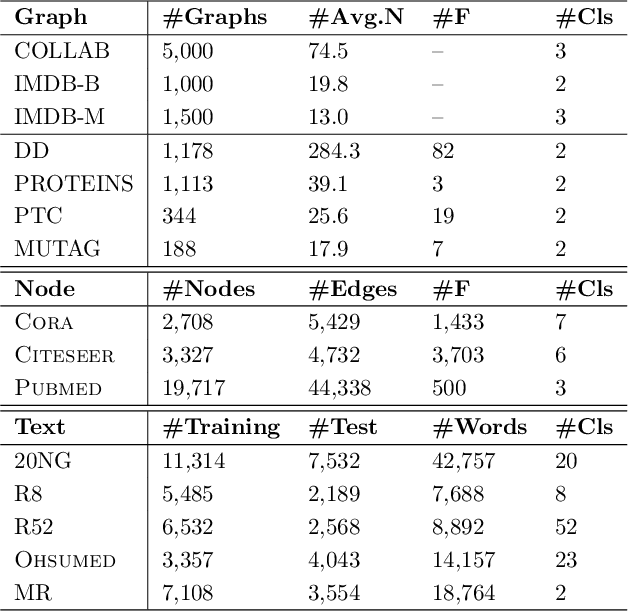
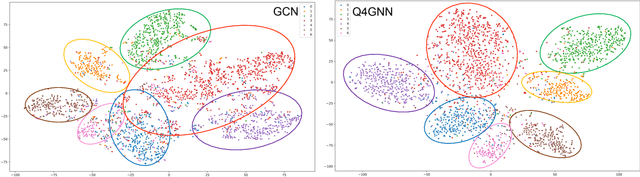
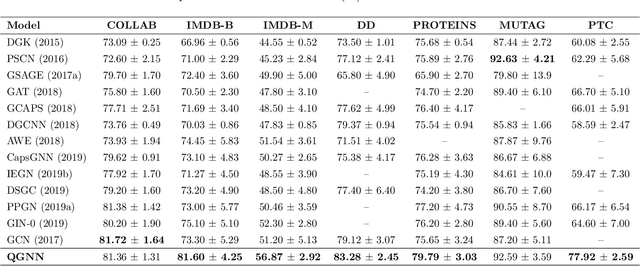
We consider reducing model parameters and moving beyond the Euclidean space to a hyper-complex space in graph neural networks (GNNs). To this end, we utilize the Quaternion space to learn quaternion node and graph embeddings. The Quaternion space, a hyper-complex space, provides highly meaningful computations through Hamilton product compared to the Euclidean and complex spaces. In particular, we propose QGNN -- a new architecture for graph neural networks which is a generalization of GCNs within the Quaternion space. QGNN reduces the model size up to four times and enhances learning graph representations. Experimental results show that our proposed QGNN produces state-of-the-art performances on a range of benchmark datasets for three downstream tasks, including graph classification, semi-supervised node classification, and text classification.