Quantum Annealing Formulation for Binary Neural Networks
Paper and Code
Jul 05, 2021
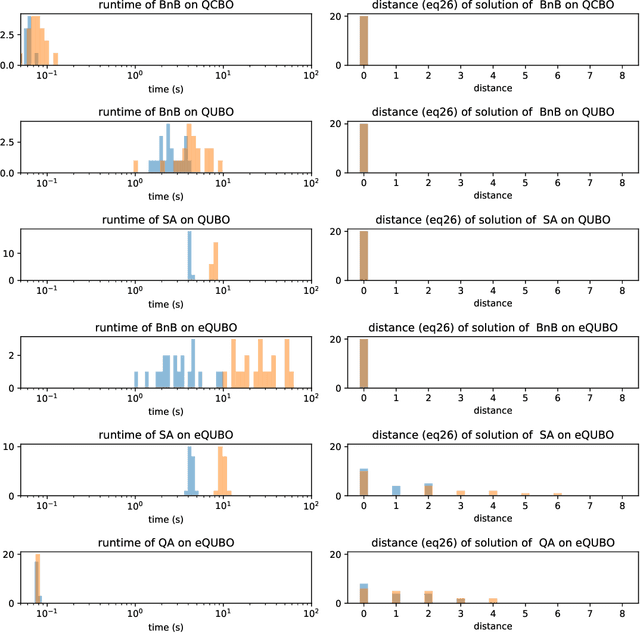
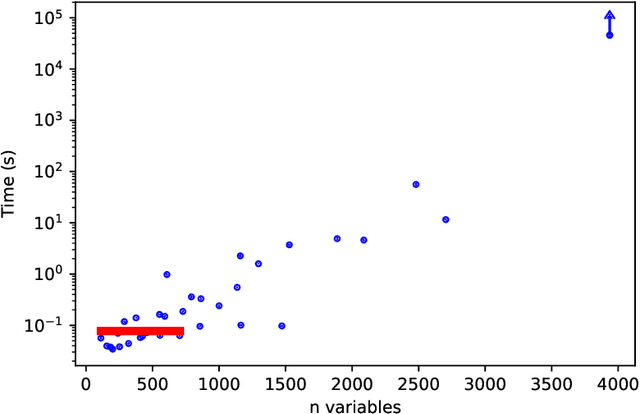

Quantum annealing is a promising paradigm for building practical quantum computers. Compared to other approaches, quantum annealing technology has been scaled up to a larger number of qubits. On the other hand, deep learning has been profoundly successful in pushing the boundaries of AI. It is thus natural to investigate potentially game changing technologies such as quantum annealers to augment the capabilities of deep learning. In this work, we explore binary neural networks, which are lightweight yet powerful models typically intended for resource constrained devices. Departing from current training regimes for binary networks that smooth/approximate the activation functions to make the network differentiable, we devise a quadratic unconstrained binary optimization formulation for the training problem. While the problem is intractable, i.e., the cost to estimate the binary weights scales exponentially with network size, we show how the problem can be optimized directly on a quantum annealer, thereby opening up to the potential gains of quantum computing. We experimentally validated our formulation via simulation and testing on an actual quantum annealer (D-Wave Advantage), the latter to the extent allowable by the capacity of current technology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge