Quantile Regression Deep Reinforcement Learning

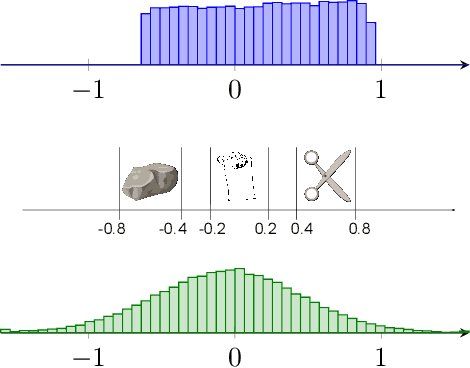
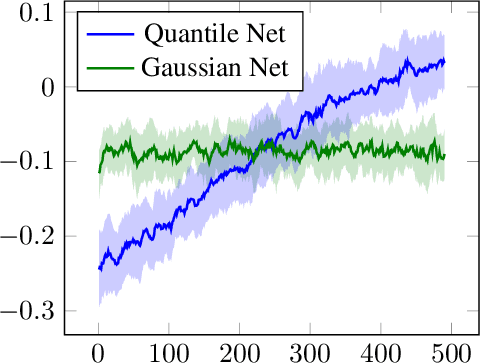
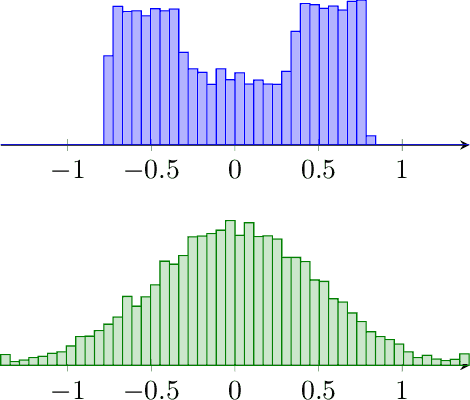
Policy gradient based reinforcement learning algorithms coupled with neural networks have shown success in learning complex policies in the model free continuous action space control setting. However, explicitly parameterized policies are limited by the scope of the chosen parametric probability distribution. We show that alternatively to the likelihood based policy gradient, a related objective can be optimized through advantage weighted quantile regression. Our approach models the policy implicitly in the network, which gives the agent the freedom to approximate any distribution in each action dimension, not limiting its capabilities to the commonly used unimodal Gaussian parameterization. This broader spectrum of policies makes our algorithm suitable for problems where Gaussian policies cannot fit the optimal policy. Moreover, our results on the MuJoCo physics simulator benchmarks are comparable or superior to state-of-the-art on-policy methods.