qecGPT: decoding Quantum Error-correcting Codes with Generative Pre-trained Transformers
Paper and Code
Jul 18, 2023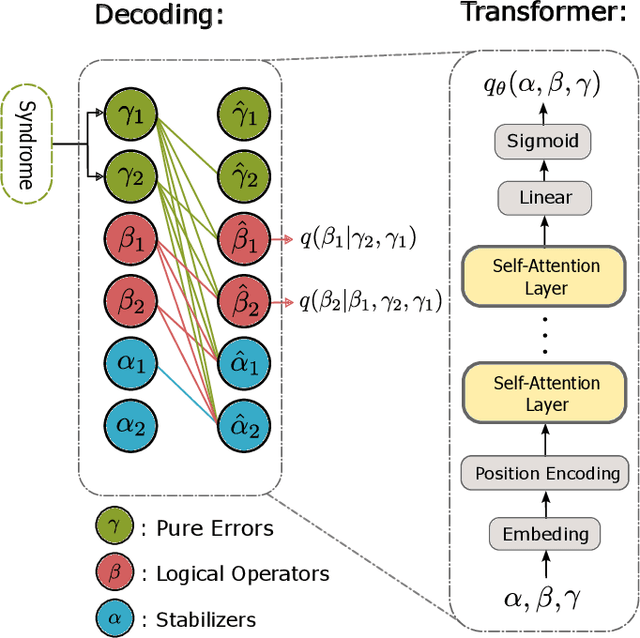
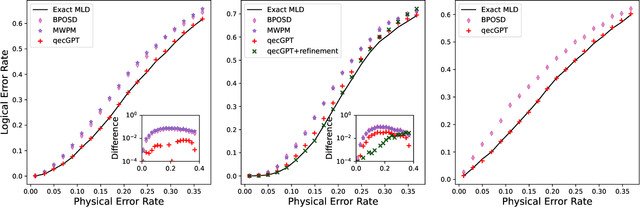
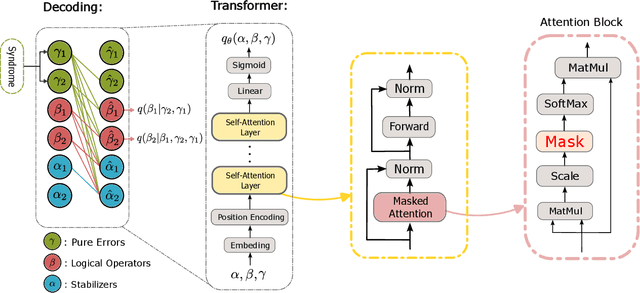
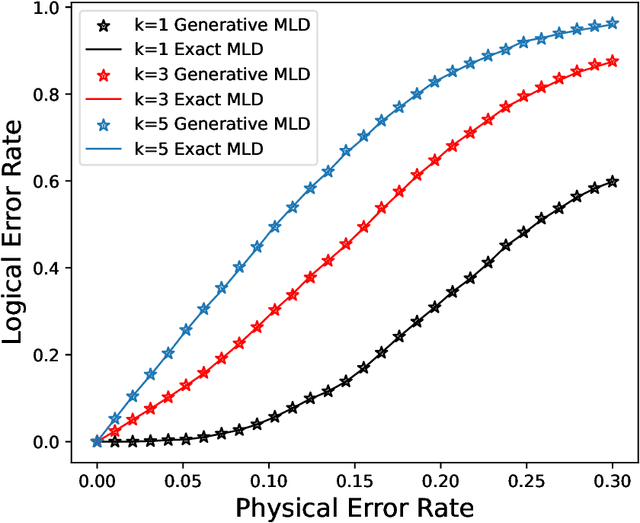
We propose a general framework for decoding quantum error-correcting codes with generative modeling. The model utilizes autoregressive neural networks, specifically Transformers, to learn the joint probability of logical operators and syndromes. This training is in an unsupervised way, without the need for labeled training data, and is thus referred to as pre-training. After the pre-training, the model can efficiently compute the likelihood of logical operators for any given syndrome, using maximum likelihood decoding. It can directly generate the most-likely logical operators with computational complexity $\mathcal O(2k)$ in the number of logical qubits $k$, which is significantly better than the conventional maximum likelihood decoding algorithms that require $\mathcal O(4^k)$ computation. Based on the pre-trained model, we further propose refinement to achieve more accurately the likelihood of logical operators for a given syndrome by directly sampling the stabilizer operators. We perform numerical experiments on stabilizer codes with small code distances, using both depolarizing error models and error models with correlated noise. The results show that our approach provides significantly better decoding accuracy than the minimum weight perfect matching and belief-propagation-based algorithms. Our framework is general and can be applied to any error model and quantum codes with different topologies such as surface codes and quantum LDPC codes. Furthermore, it leverages the parallelization capabilities of GPUs, enabling simultaneous decoding of a large number of syndromes. Our approach sheds light on the efficient and accurate decoding of quantum error-correcting codes using generative artificial intelligence and modern computational power.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge