Pursuer Assignment and Control Strategies in Multi-agent Pursuit-Evasion Under Uncertainties
Paper and Code
Mar 29, 2021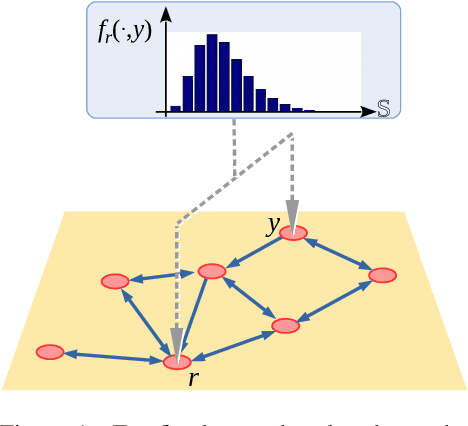
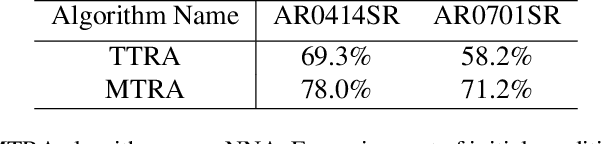
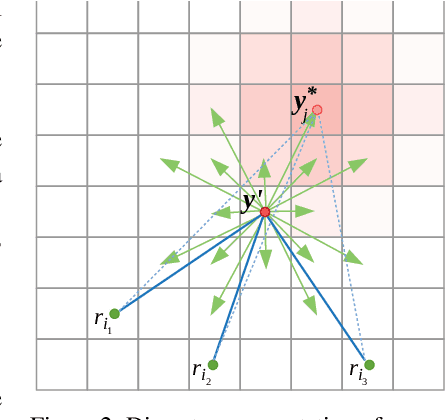
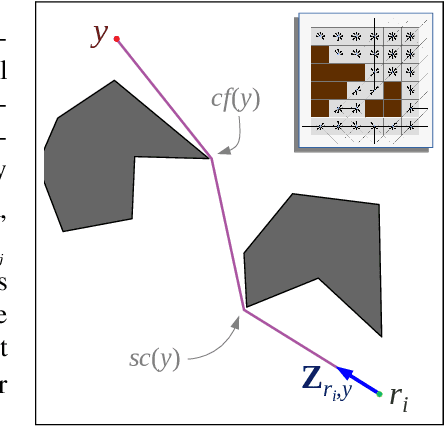
We consider a pursuit-evasion problem with a heterogeneous team of multiple pursuers and multiple evaders. Although both the pursuers (robots) and the evaders are aware of each others' control and assignment strategies, they do not have exact information about the other type of agents' location or action. Using only noisy on-board sensors the pursuers (or evaders) make probabilistic estimation of positions of the evaders (or pursuers). Each type of agent use Markov localization to update the probability distribution of the other type. A search-based control strategy is developed for the pursuers that intrinsically takes the probability distribution of the evaders into account. Pursuers are assigned using an assignment algorithm that takes redundancy (i.e., an excess in the number of pursuers than the number of evaders) into account, such that the total or maximum estimated time to capture the evaders is minimized. In this respect we assume the pursuers to have clear advantage over the evaders. However, the objective of this work is to use assignment strategies that minimize the capture time. This assignment strategy is based on a modified Hungarian algorithm as well as a novel algorithm for determining assignment of redundant pursuers. The evaders, in order to effectively avoid the pursuers, predict the assignment based on their probabilistic knowledge of the pursuers and use a control strategy to actively move away from those pursues. Our experimental evaluation shows that the redundant assignment algorithm performs better than an alternative nearest-neighbor based assignment algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge