Pure-Exploration for Infinite-Armed Bandits with General Arm Reservoirs

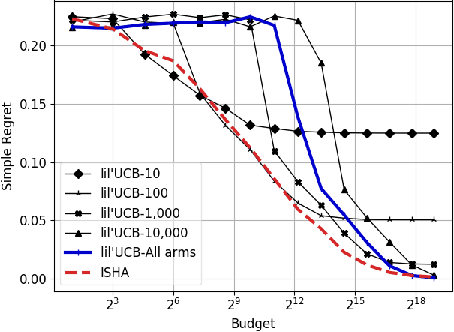
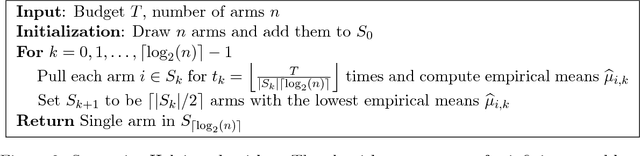
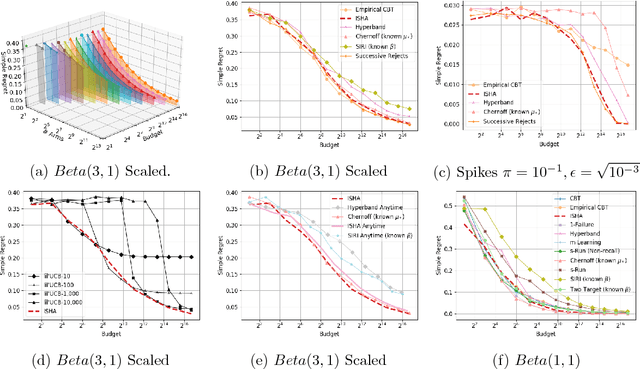
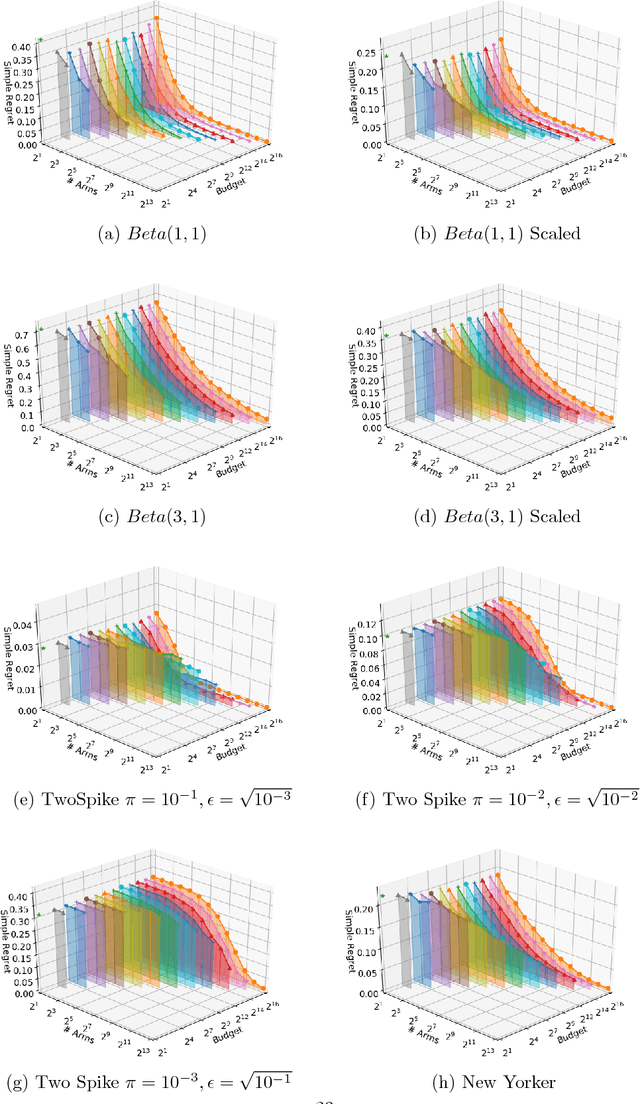
This paper considers a multi-armed bandit game where the number of arms is much larger than the maximum budget and is effectively infinite. We characterize necessary and sufficient conditions on the total budget for an algorithm to return an {\epsilon}-good arm with probability at least 1 - {\delta}. In such situations, the sample complexity depends on {\epsilon}, {\delta} and the so-called reservoir distribution {\nu} from which the means of the arms are drawn iid. While a substantial literature has developed around analyzing specific cases of {\nu} such as the beta distribution, our analysis makes no assumption about the form of {\nu}. Our algorithm is based on successive halving with the surprising exception that arms start to be discarded after just a single pull, requiring an analysis that goes beyond concentration alone. The provable correctness of this algorithm also provides an explanation for the empirical observation that the most aggressive bracket of the Hyperband algorithm of Li et al. (2017) for hyperparameter tuning is almost always best.