Pseudo value-based Deep Neural Networks for Multi-state Survival Analysis
Paper and Code
Jul 12, 2022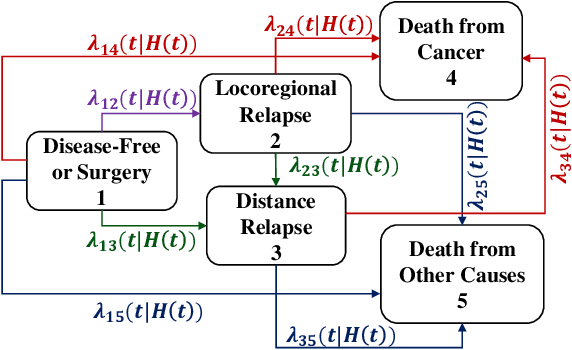
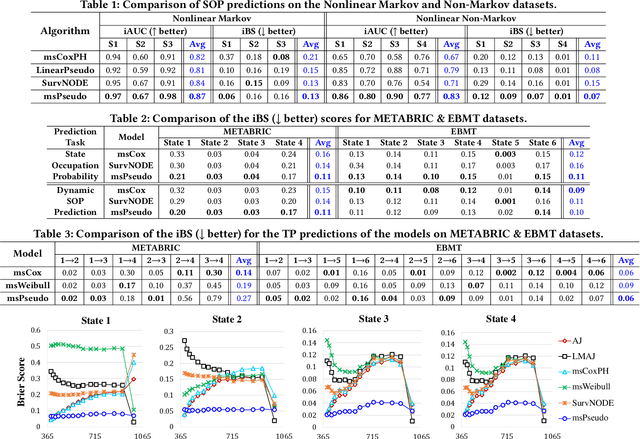
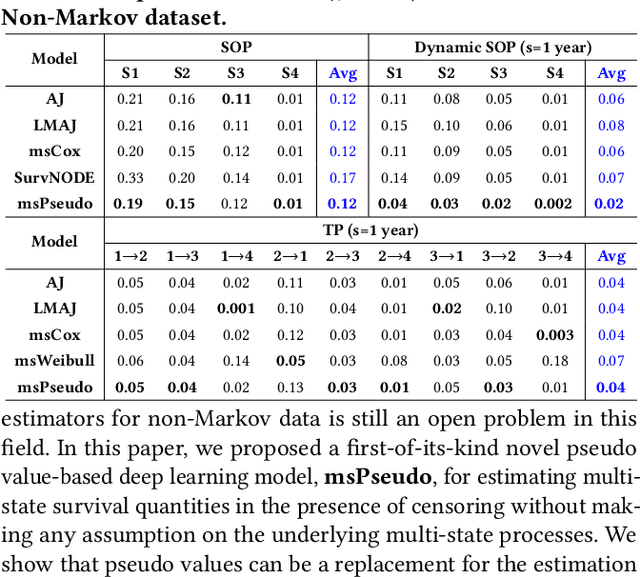
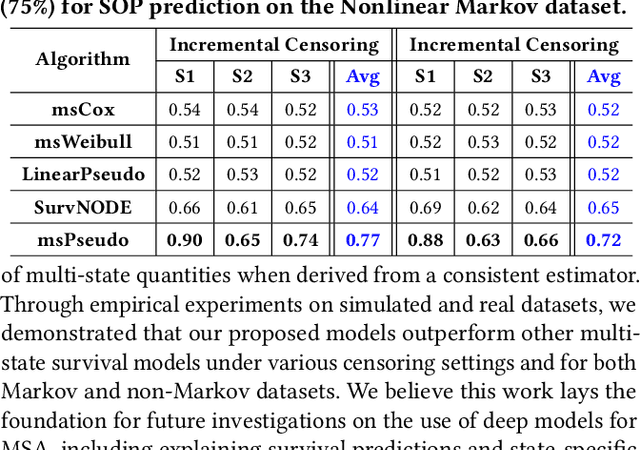
Multi-state survival analysis (MSA) uses multi-state models for the analysis of time-to-event data. In medical applications, MSA can provide insights about the complex disease progression in patients. A key challenge in MSA is the accurate subject-specific prediction of multi-state model quantities such as transition probability and state occupation probability in the presence of censoring. Traditional multi-state methods such as Aalen-Johansen (AJ) estimators and Cox-based methods are respectively limited by Markov and proportional hazards assumptions and are infeasible for making subject-specific predictions. Neural ordinary differential equations for MSA relax these assumptions but are computationally expensive and do not directly model the transition probabilities. To address these limitations, we propose a new class of pseudo-value-based deep learning models for multi-state survival analysis, where we show that pseudo values - designed to handle censoring - can be a natural replacement for estimating the multi-state model quantities when derived from a consistent estimator. In particular, we provide an algorithm to derive pseudo values from consistent estimators to directly predict the multi-state survival quantities from the subject's covariates. Empirical results on synthetic and real-world datasets show that our proposed models achieve state-of-the-art results under various censoring settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge