Provably Stable Interpretable Encodings of Context Free Grammars in RNNs with a Differentiable Stack
Paper and Code
Jun 11, 2020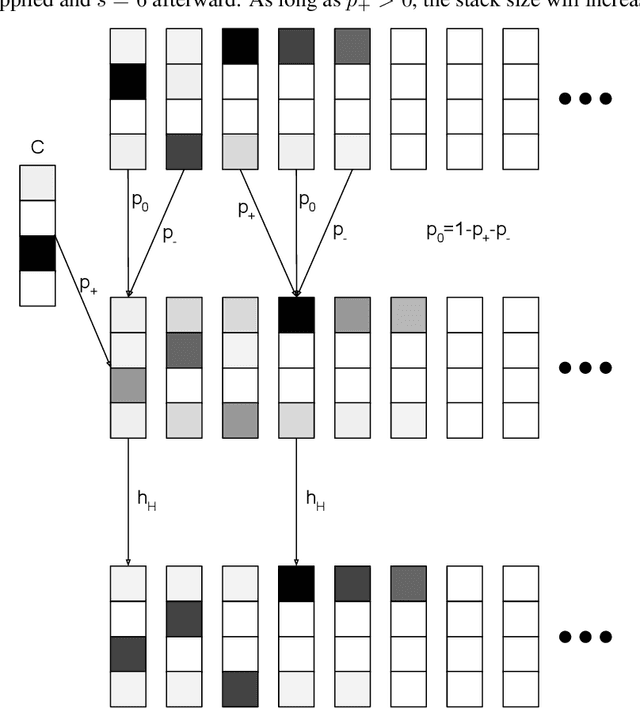
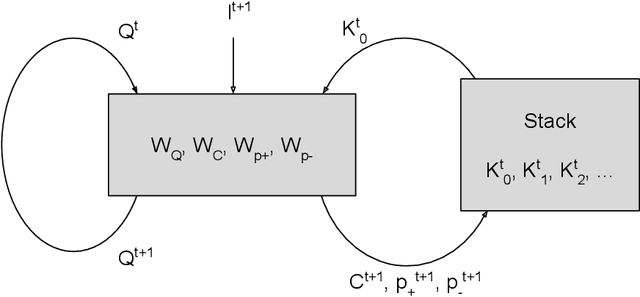
Given a collection of strings belonging to a context free grammar (CFG) and another collection of strings not belonging to the CFG, how might one infer the grammar? This is the problem of grammatical inference. Since CFGs are the languages recognized by pushdown automata (PDA), it suffices to determine the state transition rules and stack action rules of the corresponding PDA. An approach would be to train a recurrent neural network (RNN) to classify the sample data and attempt to extract these PDA rules. But neural networks are not a priori aware of the structure of a PDA and would likely require many samples to infer this structure. Furthermore, extracting the PDA rules from the RNN is nontrivial. We build a RNN specifically structured like a PDA, where weights correspond directly to the PDA rules. This requires a stack architecture that is somehow differentiable (to enable gradient-based learning) and stable (an unstable stack will show deteriorating performance with longer strings). We propose a stack architecture that is differentiable and that provably exhibits orbital stability. Using this stack, we construct a neural network that provably approximates a PDA for strings of arbitrary length. Moreover, our model and method of proof can easily be generalized to other state machines, such as a Turing Machine.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge