Provably Feasible and Stable White-Box Trajectory Optimization
Paper and Code
Jun 03, 2024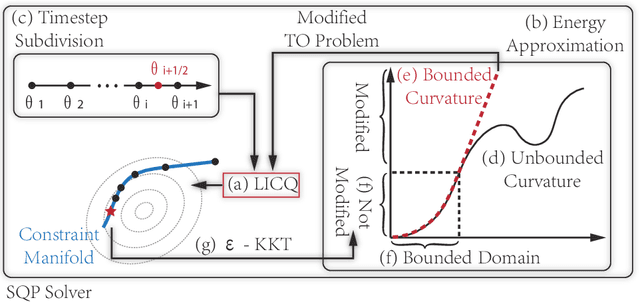
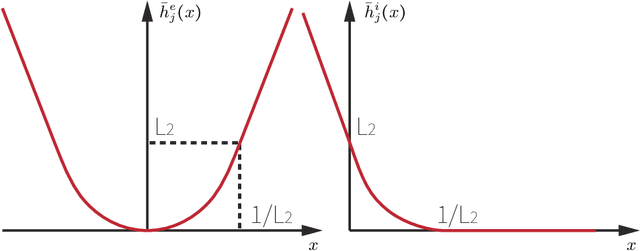
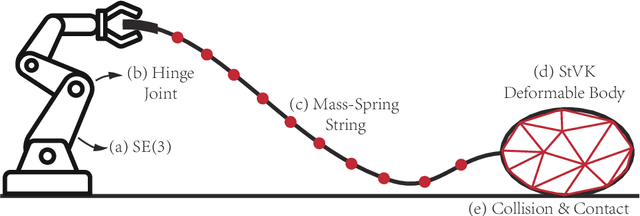

We study the problem of Trajectory Optimization (TO) for a general class of stiff and constrained dynamic systems. We establish a set of mild assumptions, under which we show that TO converges numerically stably to a locally optimal and feasible solution up to arbitrary user-specified error tolerance. Our key observation is that all prior works use SQP as a black-box solver, where a TO problem is formulated as a Nonlinear Program (NLP) and the underlying SQP solver is not allowed to modify the NLP. Instead, we propose a white-box TO solver, where the SQP solver is informed with characteristics of the objective function and the dynamic system. It then uses these characteristics to derive approximate dynamic systems and customize the discretization schemes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge