Properties of phoneme N -grams across the world's language families
Paper and Code
Jan 04, 2014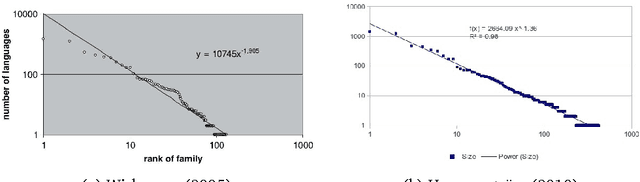

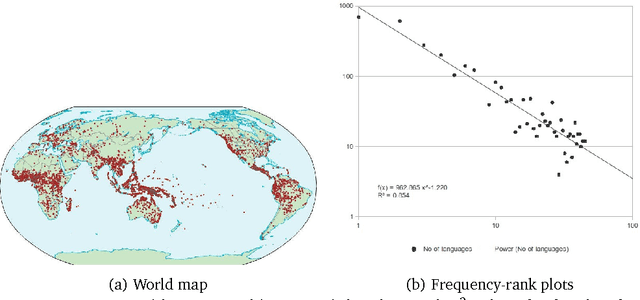
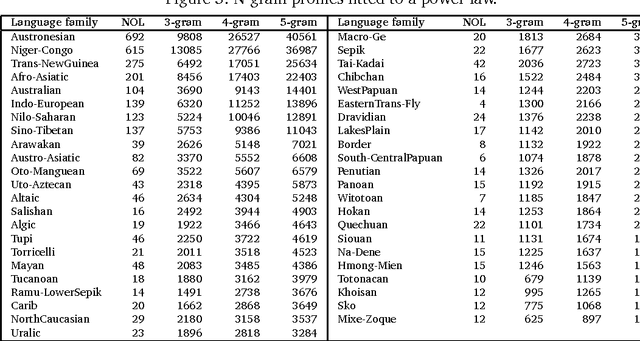
In this article, we investigate the properties of phoneme N-grams across half of the world's languages. We investigate if the sizes of three different N-gram distributions of the world's language families obey a power law. Further, the N-gram distributions of language families parallel the sizes of the families, which seem to obey a power law distribution. The correlation between N-gram distributions and language family sizes improves with increasing values of N. We applied statistical tests, originally given by physicists, to test the hypothesis of power law fit to twelve different datasets. The study also raises some new questions about the use of N-gram distributions in linguistic research, which we answer by running a statistical test.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge