Projected Gradient Descent for Spectral Compressed Sensing via Symmetric Hankel Factorization
Paper and Code
Mar 14, 2024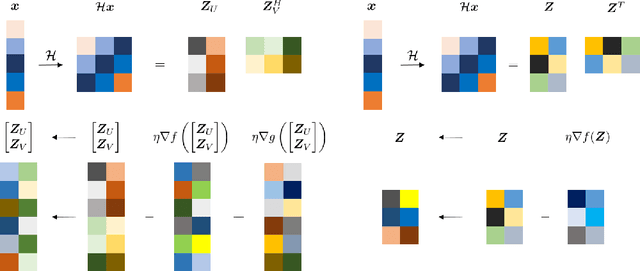


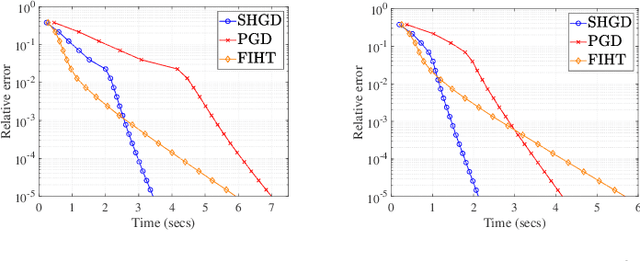
Current spectral compressed sensing methods via Hankel matrix completion employ symmetric factorization to demonstrate the low-rank property of the Hankel matrix. However, previous non-convex gradient methods only utilize asymmetric factorization to achieve spectral compressed sensing. In this paper, we propose a novel nonconvex projected gradient descent method for spectral compressed sensing via symmetric factorization named Symmetric Hankel Projected Gradient Descent (SHGD), which updates only one matrix and avoids a balancing regularization term. SHGD reduces about half of the computation and storage costs compared to the prior gradient method based on asymmetric factorization. {Besides, the symmetric factorization employed in our work is completely novel to the prior low-rank factorization model, introducing a new factorization ambiguity under complex orthogonal transformation}. Novel distance metrics are designed for our factorization method and a linear convergence guarantee to the desired signal is established with $O(r^2\log(n))$ observations. Numerical simulations demonstrate the superior performance of the proposed SHGD method in phase transitions and computation efficiency compared to state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge