Probability and Asset Updating using Bayesian Networks for Combinatorial Prediction Markets
Paper and Code
Oct 16, 2012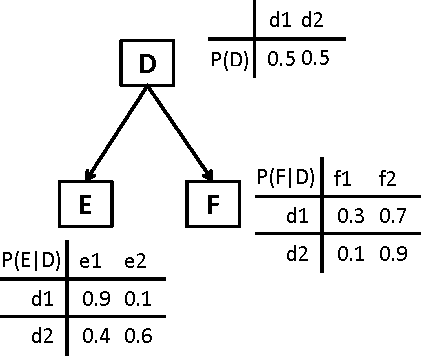

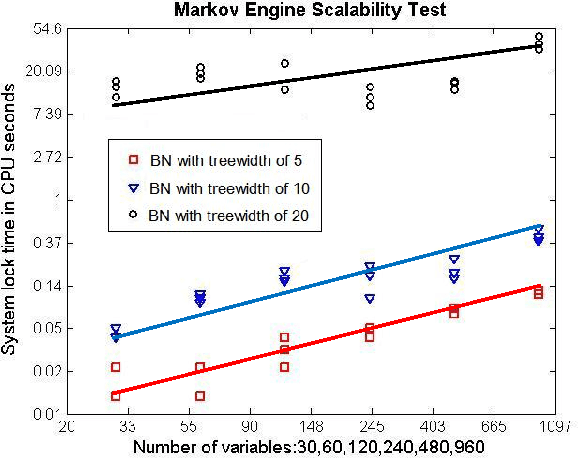
A market-maker-based prediction market lets forecasters aggregate information by editing a consensus probability distribution either directly or by trading securities that pay off contingent on an event of interest. Combinatorial prediction markets allow trading on any event that can be specified as a combination of a base set of events. However, explicitly representing the full joint distribution is infeasible for markets with more than a few base events. A factored representation such as a Bayesian network (BN) can achieve tractable computation for problems with many related variables. Standard BN inference algorithms, such as the junction tree algorithm, can be used to update a representation of the entire joint distribution given a change to any local conditional probability. However, in order to let traders reuse assets from prior trades while never allowing assets to become negative, a BN based prediction market also needs to update a representation of each user's assets and find the conditional state in which a user has minimum assets. Users also find it useful to see their expected assets given an edit outcome. We show how to generalize the junction tree algorithm to perform all these computations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge