Probabilistic transfer learning methodology to expedite high fidelity simulation of reactive flows
Paper and Code
May 17, 2024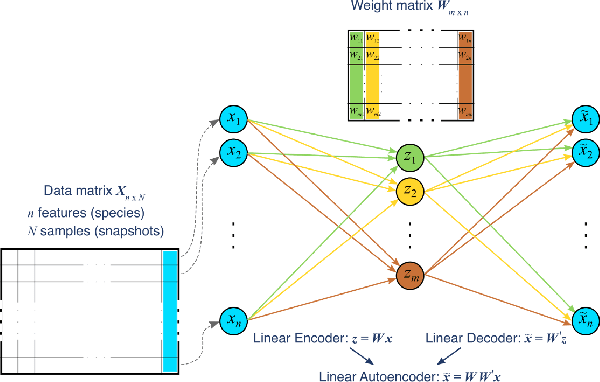
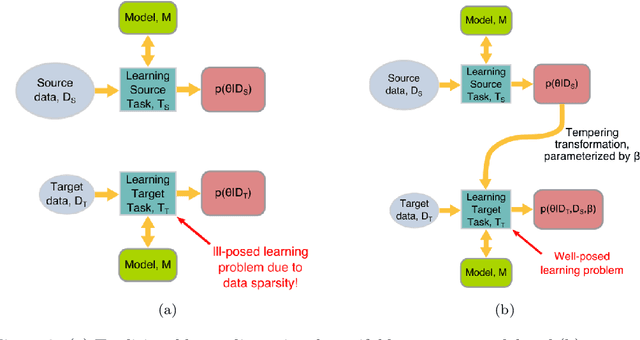
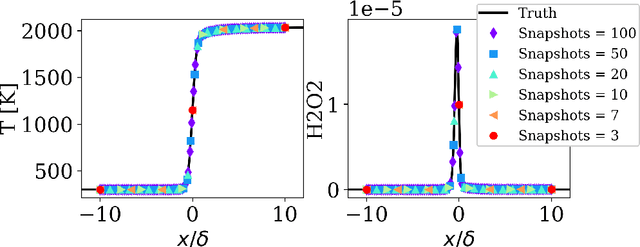
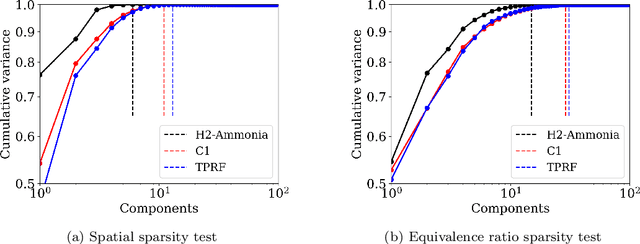
Reduced order models based on the transport of a lower dimensional manifold representation of the thermochemical state, such as Principal Component (PC) transport and Machine Learning (ML) techniques, have been developed to reduce the computational cost associated with the Direct Numerical Simulations (DNS) of reactive flows. Both PC transport and ML normally require an abundance of data to exhibit sufficient predictive accuracy, which might not be available due to the prohibitive cost of DNS or experimental data acquisition. To alleviate such difficulties, similar data from an existing dataset or domain (source domain) can be used to train ML models, potentially resulting in adequate predictions in the domain of interest (target domain). This study presents a novel probabilistic transfer learning (TL) framework to enhance the trust in ML models in correctly predicting the thermochemical state in a lower dimensional manifold and a sparse data setting. The framework uses Bayesian neural networks, and autoencoders, to reduce the dimensionality of the state space and diffuse the knowledge from the source to the target domain. The new framework is applied to one-dimensional freely-propagating flame solutions under different data sparsity scenarios. The results reveal that there is an optimal amount of knowledge to be transferred, which depends on the amount of data available in the target domain and the similarity between the domains. TL can reduce the reconstruction error by one order of magnitude for cases with large sparsity. The new framework required 10 times less data for the target domain to reproduce the same error as in the abundant data scenario. Furthermore, comparisons with a state-of-the-art deterministic TL strategy show that the probabilistic method can require four times less data to achieve the same reconstruction error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge