Probabilistic hypergraph grammars for efficient molecular optimization
Paper and Code
Jun 05, 2019
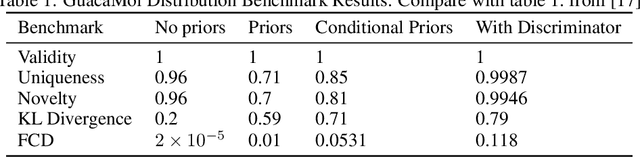
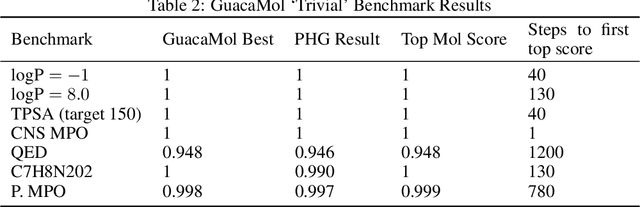
We present an approach to make molecular optimization more efficient. We infer a hypergraph replacement grammar from the ChEMBL database, count the frequencies of particular rules being used to expand particular nonterminals in other rules, and use these as conditional priors for the policy model. Simulating random molecules from the resulting probabilistic grammar, we show that conditional priors result in a molecular distribution closer to the training set than using equal rule probabilities or unconditional priors. We then treat molecular optimization as a reinforcement learning problem, using a novel modification of the policy gradient algorithm - batch-advantage: using individual rewards minus the batch average reward to weight the log probability loss. The reinforcement learning agent is tasked with building molecules using this grammar, with the goal of maximizing benchmark scores available from the literature. To do so, the agent has policies both to choose the next node in the graph to expand and to select the next grammar rule to apply. The policies are implemented using the Transformer architecture with the partially expanded graph as the input at each step. We show that using the empirical priors as the starting point for a policy eliminates the need for pre-training, and allows us to reach optima faster. We achieve competitive performance on common benchmarks from the literature, such as penalized logP and QED, with only hundreds of training steps on a budget GPU instance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge