Private Q-Learning with Functional Noise in Continuous Spaces

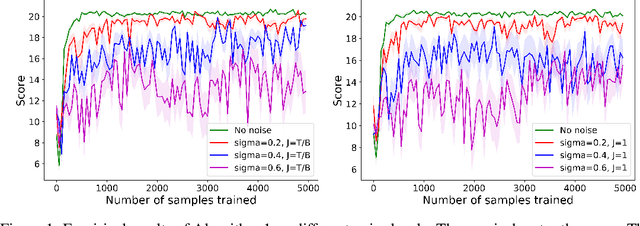
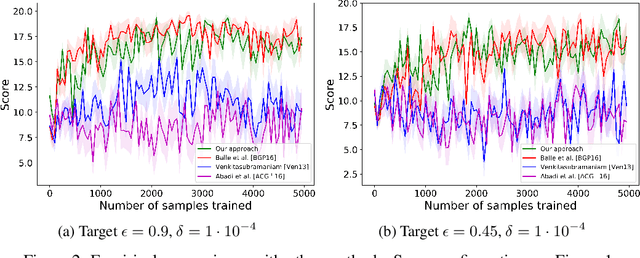
We consider privacy-preserving algorithms for deep reinforcement learning. State-of-the-art methods that guarantee differential privacy are not extendable to very large state spaces because the noise level necessary to ensure privacy would scale to infinity. We address the problem of providing differential privacy in Q-learning where a function approximation through a neural network is used for parametrization. We develop a rigorous and efficient algorithm by inspecting the reproducing kernel Hilbert space in which the neural network is embedded. Our approach uses functional noise to guarantee privacy, while the noise level scales linearly with the complexity of the neural network architecture. There are no known theoretical guarantees on the performance of deep reinforcement learning, but we gain some insight by providing a utility analysis under the discrete space setting.