Private Domain Adaptation from a Public Source
Paper and Code
Aug 12, 2022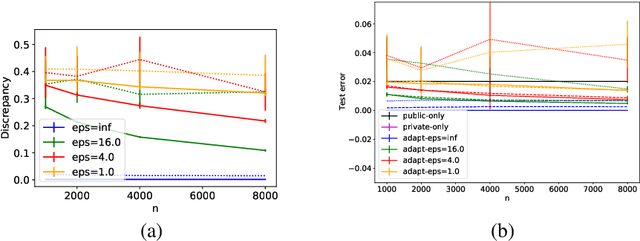
A key problem in a variety of applications is that of domain adaptation from a public source domain, for which a relatively large amount of labeled data with no privacy constraints is at one's disposal, to a private target domain, for which a private sample is available with very few or no labeled data. In regression problems with no privacy constraints on the source or target data, a discrepancy minimization algorithm based on several theoretical guarantees was shown to outperform a number of other adaptation algorithm baselines. Building on that approach, we design differentially private discrepancy-based algorithms for adaptation from a source domain with public labeled data to a target domain with unlabeled private data. The design and analysis of our private algorithms critically hinge upon several key properties we prove for a smooth approximation of the weighted discrepancy, such as its smoothness with respect to the $\ell_1$-norm and the sensitivity of its gradient. Our solutions are based on private variants of Frank-Wolfe and Mirror-Descent algorithms. We show that our adaptation algorithms benefit from strong generalization and privacy guarantees and report the results of experiments demonstrating their effectiveness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge