Privacy-Preserving Adversarial Network (PPAN) for Continuous non-Gaussian Attributes
Paper and Code
Mar 11, 2020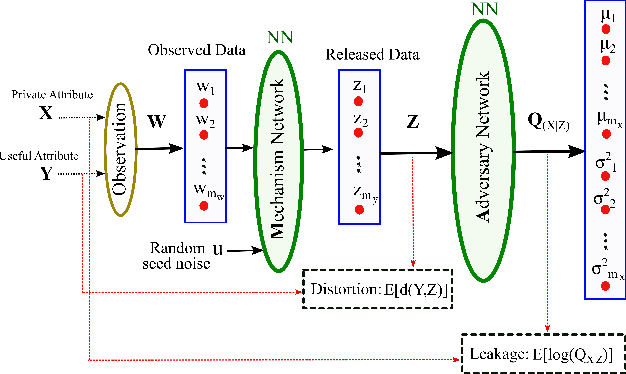
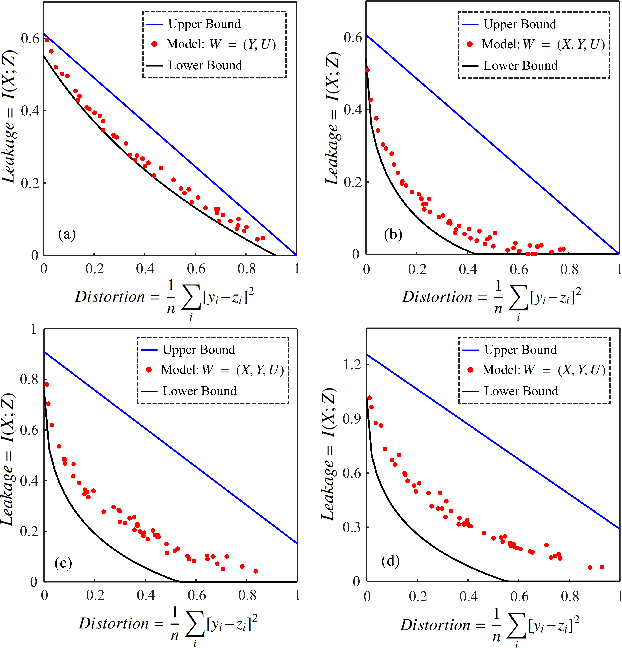
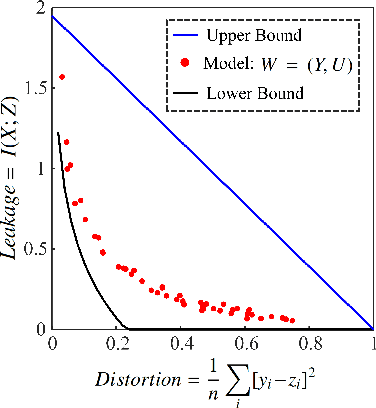
A privacy-preserving adversarial network (PPAN) was recently proposed as an information-theoretical framework to address the issue of privacy in data sharing. The main idea of this model was using mutual information as the privacy measure and adversarial training of two deep neural networks, one as the mechanism and another as the adversary. The performance of the PPAN model for the discrete synthetic data, MNIST handwritten digits, and continuous Gaussian data was evaluated compared to the analytically optimal trade-off. In this study, we evaluate the PPAN model for continuous non-Gaussian data where lower and upper bounds of the privacy-preserving problem are used. These bounds include the Kraskov (KSG) estimation of entropy and mutual information that is based on k-th nearest neighbor. In addition to the synthetic data sets, a practical case for hiding the actual electricity consumption from smart meter readings is examined. The results show that for continuous non-Gaussian data, the PPAN model performs within the determined optimal ranges and close to the lower bound.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge