Principled Uncertainty Estimation for Deep Neural Networks

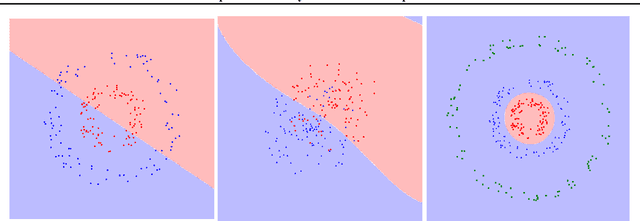
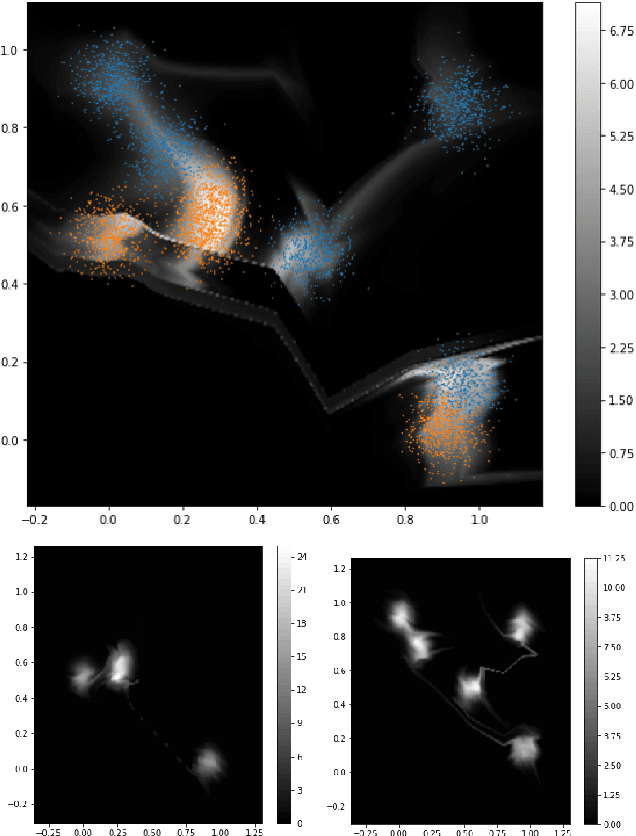
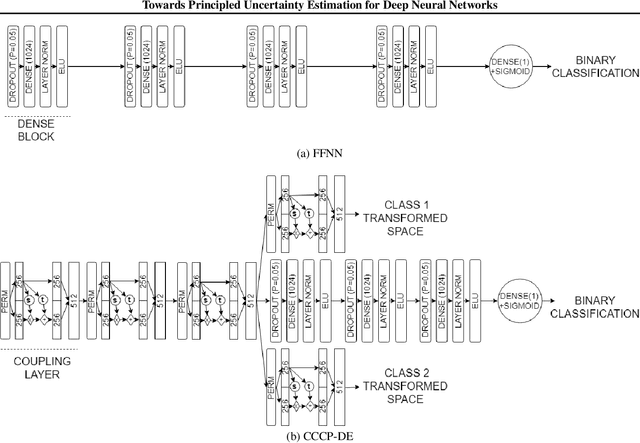
When the cost of misclassifying a sample is high, it is useful to have an accurate estimate of uncertainty in the prediction for that sample. There are also multiple types of uncertainty which are best estimated in different ways, for example, uncertainty that is intrinsic to the training set may be well-handled by a Bayesian approach, while uncertainty introduced by shifts between training and query distributions may be better-addressed by density/support estimation. In this paper, we examine three types of uncertainty: model capacity uncertainty, intrinsic data uncertainty, and open set uncertainty, and review techniques that have been derived to address each one. We then introduce a unified hierarchical model, which combines methods from Bayesian inference, invertible latent density inference, and discriminative classification in a single end-to-end deep neural network topology to yield efficient per-sample uncertainty estimation. Our approach addresses all three uncertainty types and readily accommodates prior/base rates for binary detection.