Pretending Fair Decisions via Stealthily Biased Sampling
Paper and Code
Jan 24, 2019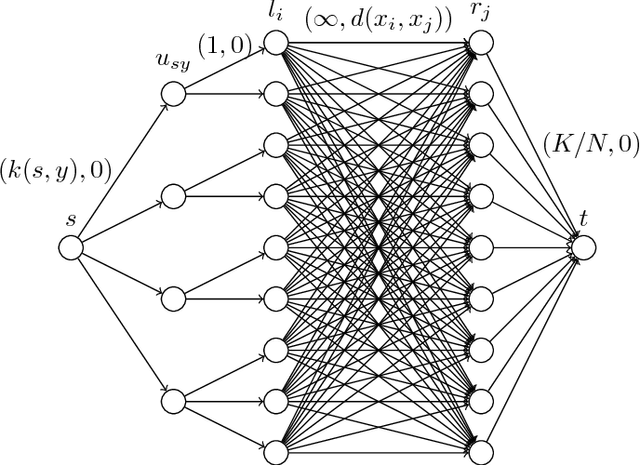
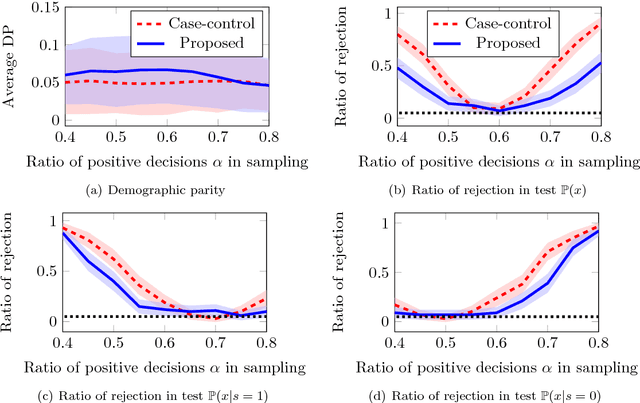
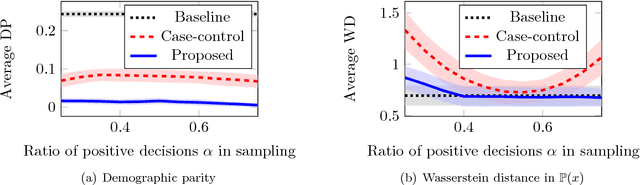
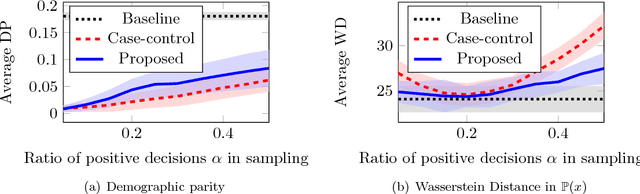
Fairness by decision-makers is believed to be auditable by third parties. In this study, we show that this is not always true. We consider the following scenario. Imagine a decision-maker who discloses a subset of his dataset with decisions to make his decisions auditable. If he is corrupt, and he deliberately selects a subset that looks fair even though the overall decision is unfair, can we identify this decision-maker's fraud? We answer this question negatively. We first propose a sampling method that produces a subset whose distribution is biased from the original (to pretend to be fair); however, its differentiation from uniform sampling is difficult. We call such a sampling method as stealthily biased sampling, which is formulated as a Wasserstein distance minimization problem, and is solved through a minimum-cost flow computation. We proved that the stealthily biased sampling minimizes an upper-bound of the indistinguishability. We conducted experiments to see that the stealthily biased sampling is, in fact, difficult to detect.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge