Preference fusion and Condorcet's Paradox under uncertainty
Paper and Code
Aug 09, 2017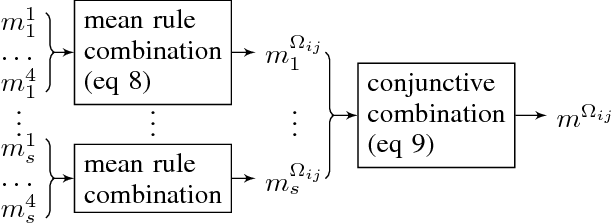



Facing an unknown situation, a person may not be able to firmly elicit his/her preferences over different alternatives, so he/she tends to express uncertain preferences. Given a community of different persons expressing their preferences over certain alternatives under uncertainty, to get a collective representative opinion of the whole community, a preference fusion process is required. The aim of this work is to propose a preference fusion method that copes with uncertainty and escape from the Condorcet paradox. To model preferences under uncertainty, we propose to develop a model of preferences based on belief function theory that accurately describes and captures the uncertainty associated with individual or collective preferences. This work improves and extends the previous results. This work improves and extends the contribution presented in a previous work. The benefits of our contribution are twofold. On the one hand, we propose a qualitative and expressive preference modeling strategy based on belief-function theory which scales better with the number of sources. On the other hand, we propose an incremental distance-based algorithm (using Jousselme distance) for the construction of the collective preference order to avoid the Condorcet Paradox.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge