Predictive Neural Networks

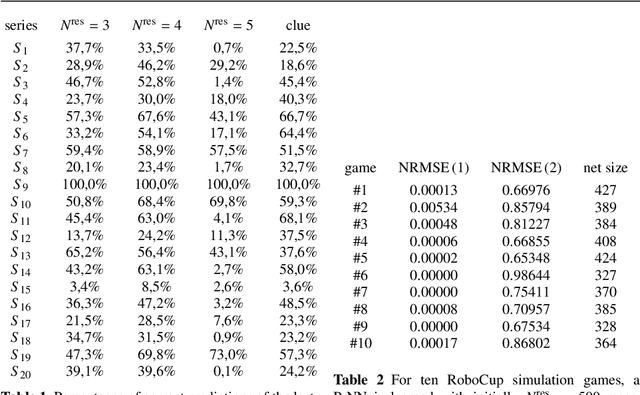
Recurrent neural networks are a powerful means to cope with time series. We show that already linearly activated recurrent neural networks can approximate any time-dependent function f(t) given by a number of function values. The approximation can effectively be learned by simply solving a linear equation system; no backpropagation or similar methods are needed. Furthermore, the network size can be reduced by taking only the most relevant components of the network. Thus, in contrast to others, our approach not only learns network weights but also the network architecture. The networks have interesting properties: In the stationary case they end up in ellipse trajectories in the long run, and they allow the prediction of further values and compact representations of functions. We demonstrate this by several experiments, among them multiple superimposed oscillators (MSO) and robotic soccer. Predictive neural networks outperform the previous state-of-the-art for the MSO task with a minimal number of units.