Prediction and Modularity in Dynamical Systems
Paper and Code
Jan 16, 2015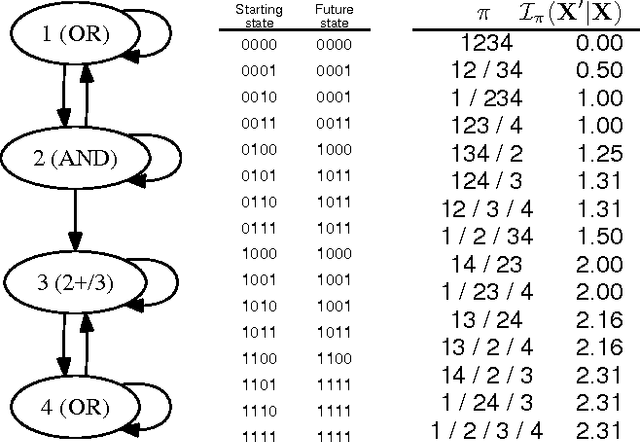
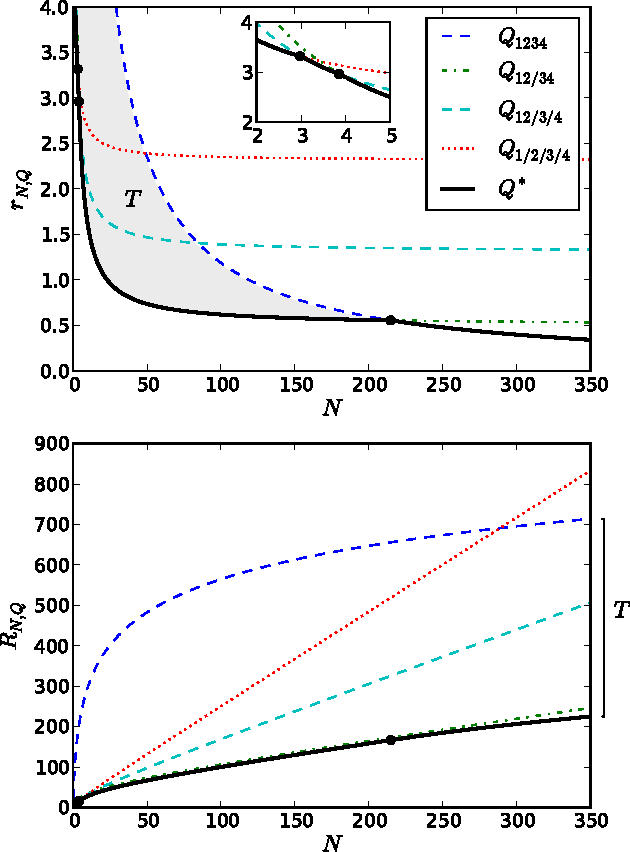
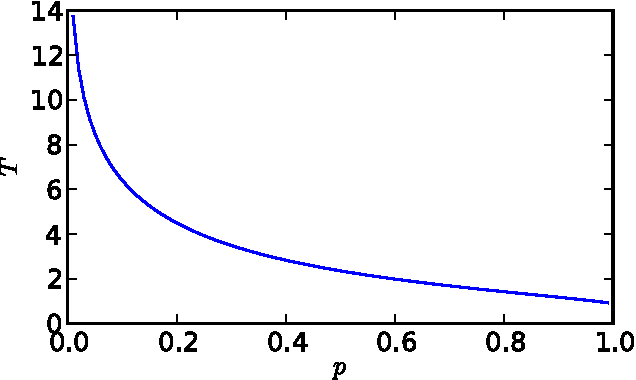
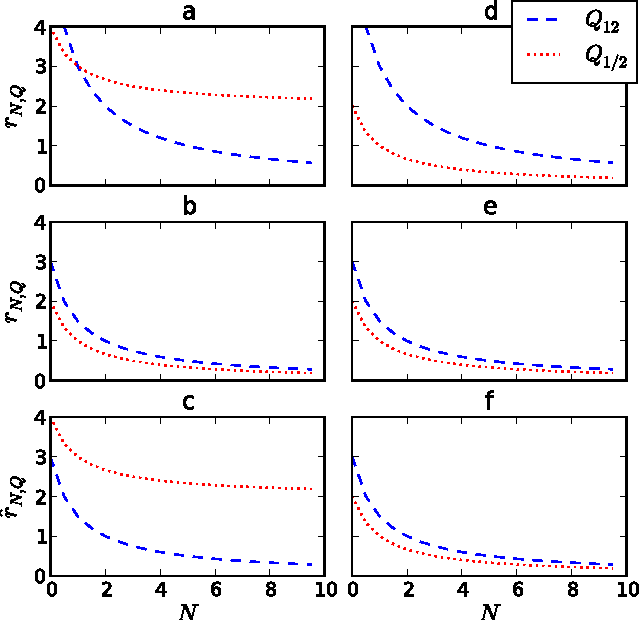
Identifying and understanding modular organizations is centrally important in the study of complex systems. Several approaches to this problem have been advanced, many framed in information-theoretic terms. Our treatment starts from the complementary point of view of statistical modeling and prediction of dynamical systems. It is known that for finite amounts of training data, simpler models can have greater predictive power than more complex ones. We use the trade-off between model simplicity and predictive accuracy to generate optimal multiscale decompositions of dynamical networks into weakly-coupled, simple modules. State-dependent and causal versions of our method are also proposed.
* v1 published in ECAL 2011 (European Conference on Artificial Life).
v2 fixes error in causal risk (number of parameters should be based on
training distribution)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge