Predicting Out-of-Domain Generalization with Local Manifold Smoothness
Paper and Code
Jul 17, 2022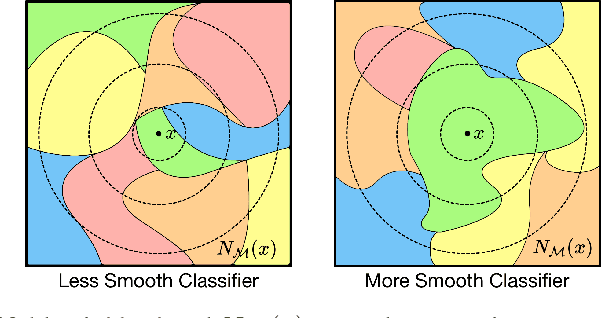
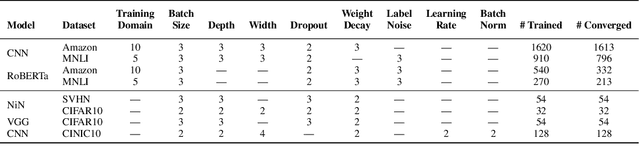

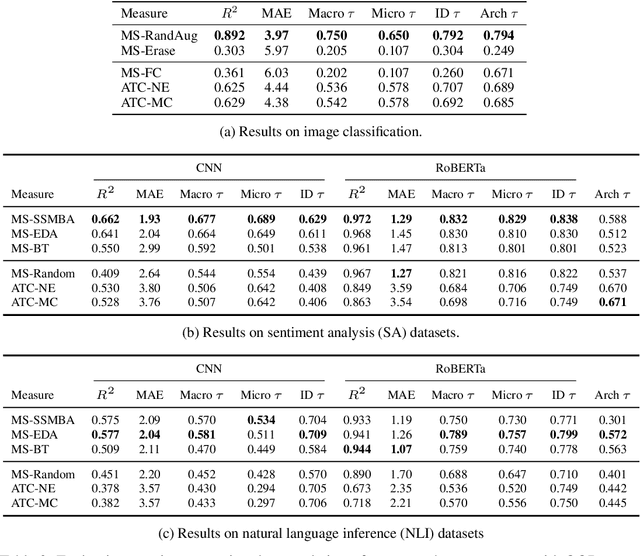
Understanding how machine learning models generalize to new environments is a critical part of their safe deployment. Recent work has proposed a variety of complexity measures that directly predict or theoretically bound the generalization capacity of a model. However, these methods rely on a strong set of assumptions that in practice are not always satisfied. Motivated by the limited settings in which existing measures can be applied, we propose a novel complexity measure based on the local manifold smoothness of a classifier. We define local manifold smoothness as a classifier's output sensitivity to perturbations in the manifold neighborhood around a given test point. Intuitively, a classifier that is less sensitive to these perturbations should generalize better. To estimate smoothness we sample points using data augmentation and measure the fraction of these points classified into the majority class. Our method only requires selecting a data augmentation method and makes no other assumptions about the model or data distributions, meaning it can be applied even in out-of-domain (OOD) settings where existing methods cannot. In experiments on robustness benchmarks in image classification, sentiment analysis, and natural language inference, we demonstrate a strong and robust correlation between our manifold smoothness measure and actual OOD generalization on over 3,000 models evaluated on over 100 train/test domain pairs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge