Practical Bayesian Optimization for Model Fitting with Bayesian Adaptive Direct Search
Paper and Code
Nov 02, 2017
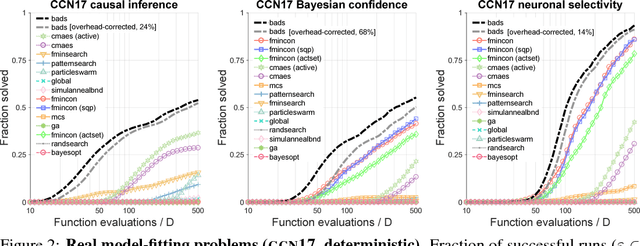

Computational models in fields such as computational neuroscience are often evaluated via stochastic simulation or numerical approximation. Fitting these models implies a difficult optimization problem over complex, possibly noisy parameter landscapes. Bayesian optimization (BO) has been successfully applied to solving expensive black-box problems in engineering and machine learning. Here we explore whether BO can be applied as a general tool for model fitting. First, we present a novel hybrid BO algorithm, Bayesian adaptive direct search (BADS), that achieves competitive performance with an affordable computational overhead for the running time of typical models. We then perform an extensive benchmark of BADS vs. many common and state-of-the-art nonconvex, derivative-free optimizers, on a set of model-fitting problems with real data and models from six studies in behavioral, cognitive, and computational neuroscience. With default settings, BADS consistently finds comparable or better solutions than other methods, including `vanilla' BO, showing great promise for advanced BO techniques, and BADS in particular, as a general model-fitting tool.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge