ppAUC: Privacy Preserving Area Under the Curve with Secure 3-Party Computation

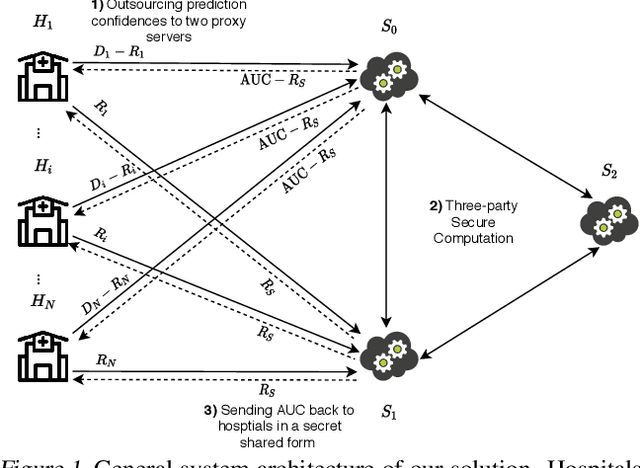
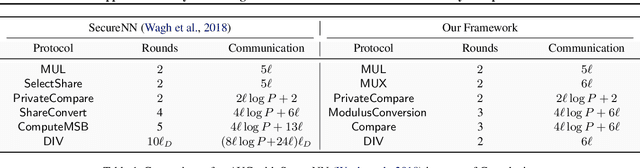
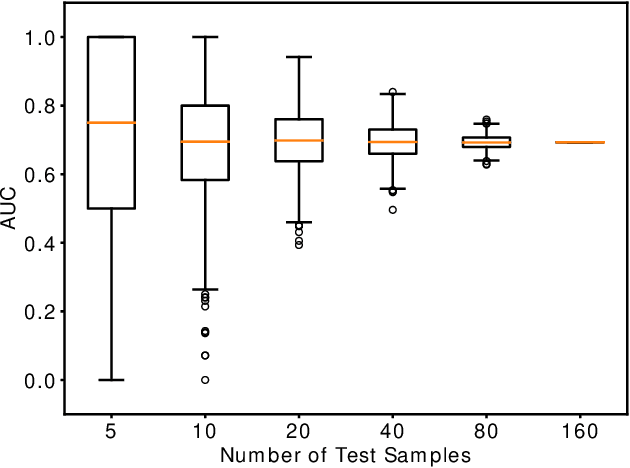
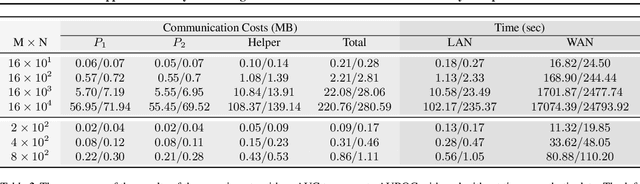
Computing an AUC as a performance measure to compare the quality of different machine learning models is one of the final steps of many research projects. Many of these methods are trained on privacy-sensitive data and there are several different approaches like $\epsilon$-differential privacy, federated machine learning and methods based on cryptographic approaches if the datasets cannot be shared or evaluated jointly at one place. In this setting, it can also be a problem to compute the global AUC, since the labels might also contain privacy-sensitive information. There have been approaches based on $\epsilon$-differential privacy to deal with this problem, but to the best of our knowledge, no exact privacy preserving solution has been introduced. In this paper, we propose an MPC-based framework, called privacy preserving AUC (ppAUC), with novel methods for comparing two secret-shared values, selecting between two secret-shared values, converting the modulus and performing division to compute the exact AUC as one could obtain on the pooled original test samples. We employ ppAUC in the computation of the exact area under precision-recall curve and receiver operating characteristic curve even for ties between prediction confidence values. To prove the correctness of ppAUC, we apply it to evaluate a model trained to predict acute myeloid leukemia therapy response and we also assess its scalability via experiments on synthetic data. The experiments show that we efficiently compute exactly the same AUC with both evaluation metrics in a privacy preserving manner as one can obtain on the pooled test samples in the plaintext domain. Our solution provides security against semi-honest corruption of at most one of the servers performing the secure computation.