power-law nonlinearity with maximally uniform distribution criterion for improved neural network training in automatic speech recognition
Paper and Code
Dec 22, 2019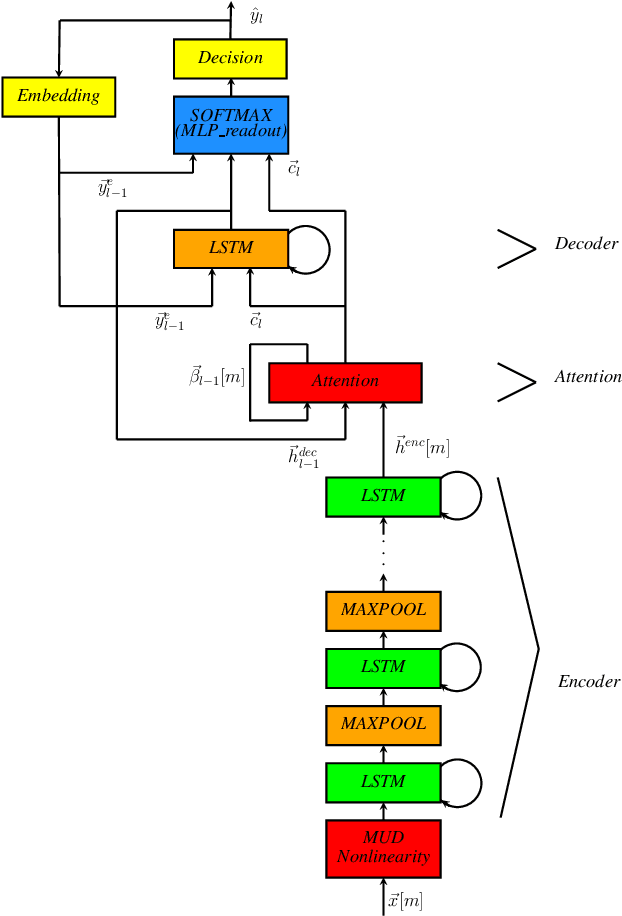
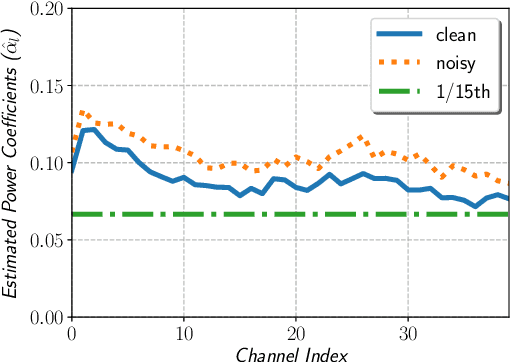
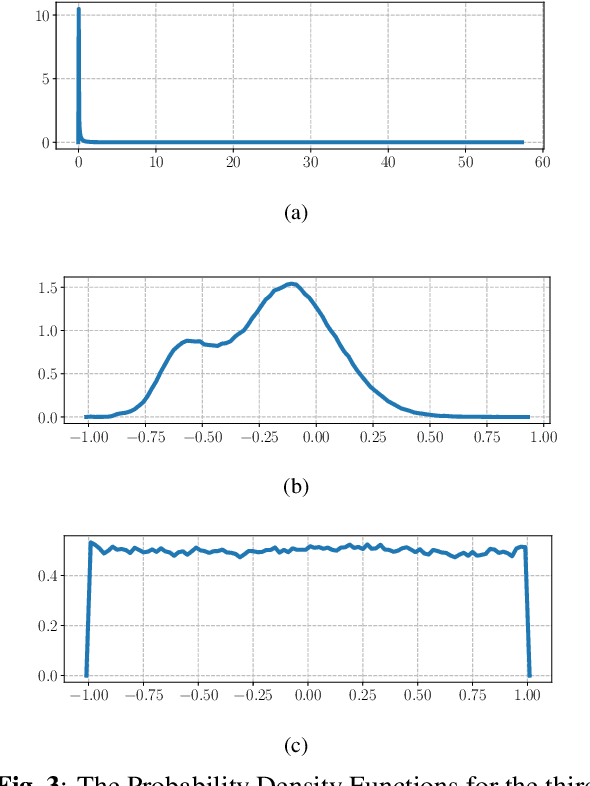
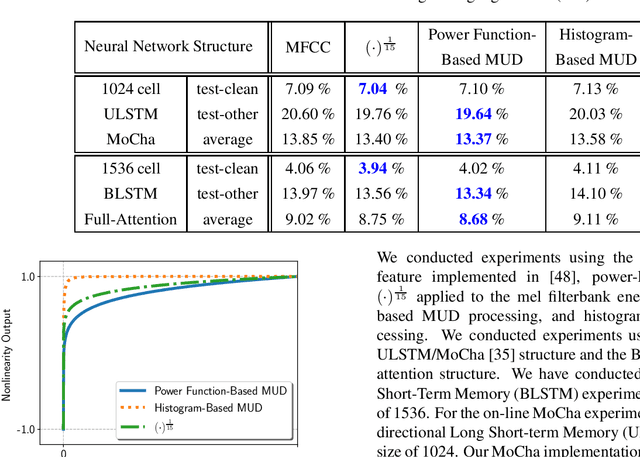
In this paper, we describe the Maximum Uniformity of Distribution (MUD) algorithm with the power-law nonlinearity. In this approach, we hypothesize that neural network training will become more stable if feature distribution is not too much skewed. We propose two different types of MUD approaches: power function-based MUD and histogram-based MUD. In these approaches, we first obtain the mel filterbank coefficients and apply nonlinearity functions for each filterbank channel. With the power function-based MUD, we apply a power-function based nonlinearity where power function coefficients are chosen to maximize the likelihood assuming that nonlinearity outputs follow the uniform distribution. With the histogram-based MUD, the empirical Cumulative Density Function (CDF) from the training database is employed to transform the original distribution into a uniform distribution. In MUD processing, we do not use any prior knowledge (e.g. logarithmic relation) about the energy of the incoming signal and the perceived intensity by a human. Experimental results using an end-to-end speech recognition system demonstrate that power-function based MUD shows better result than the conventional Mel Filterbank Cepstral Coefficients (MFCCs). On the LibriSpeech database, we could achieve 4.02 % WER on test-clean and 13.34 % WER on test-other without using any Language Models (LMs). The major contribution of this work is that we developed a new algorithm for designing the compressive nonlinearity in a data-driven way, which is much more flexible than the previous approaches and may be extended to other domains as well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge