Positive Semidefinite Metric Learning Using Boosting-like Algorithms

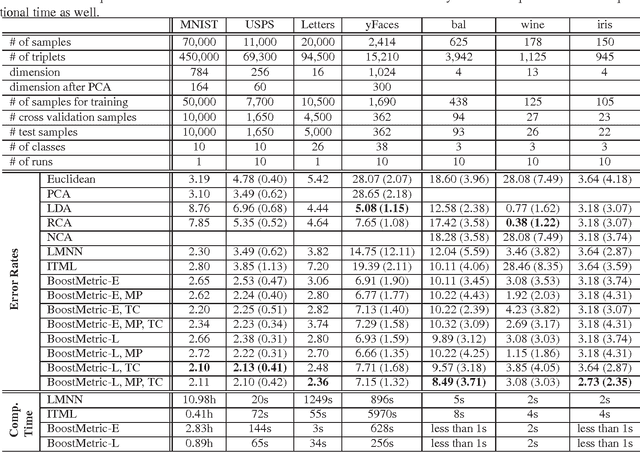
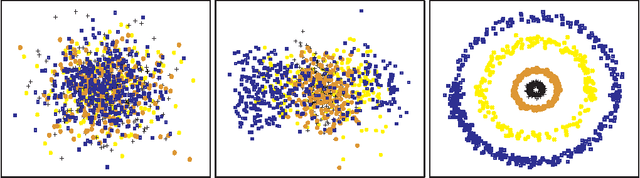
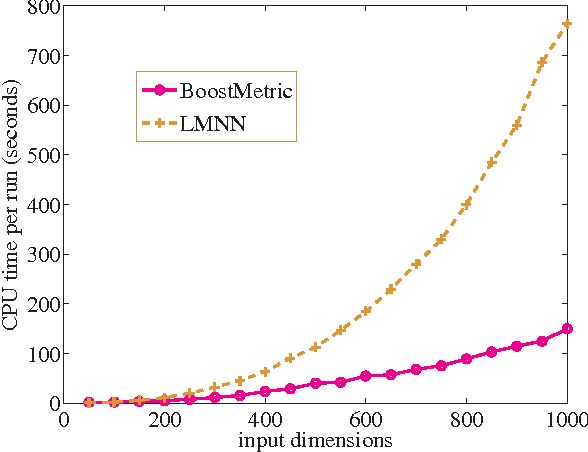
The success of many machine learning and pattern recognition methods relies heavily upon the identification of an appropriate distance metric on the input data. It is often beneficial to learn such a metric from the input training data, instead of using a default one such as the Euclidean distance. In this work, we propose a boosting-based technique, termed BoostMetric, for learning a quadratic Mahalanobis distance metric. Learning a valid Mahalanobis distance metric requires enforcing the constraint that the matrix parameter to the metric remains positive definite. Semidefinite programming is often used to enforce this constraint, but does not scale well and easy to implement. BoostMetric is instead based on the observation that any positive semidefinite matrix can be decomposed into a linear combination of trace-one rank-one matrices. BoostMetric thus uses rank-one positive semidefinite matrices as weak learners within an efficient and scalable boosting-based learning process. The resulting methods are easy to implement, efficient, and can accommodate various types of constraints. We extend traditional boosting algorithms in that its weak learner is a positive semidefinite matrix with trace and rank being one rather than a classifier or regressor. Experiments on various datasets demonstrate that the proposed algorithms compare favorably to those state-of-the-art methods in terms of classification accuracy and running time.