Policy Learning of MDPs with Mixed Continuous/Discrete Variables: A Case Study on Model-Free Control of Markovian Jump Systems
Paper and Code
Jun 04, 2020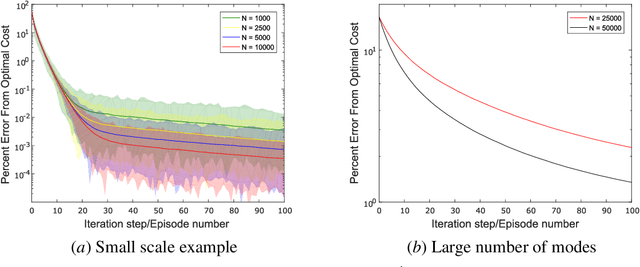
Markovian jump linear systems (MJLS) are an important class of dynamical systems that arise in many control applications. In this paper, we introduce the problem of controlling unknown (discrete-time) MJLS as a new benchmark for policy-based reinforcement learning of Markov decision processes (MDPs) with mixed continuous/discrete state variables. Compared with the traditional linear quadratic regulator (LQR), our proposed problem leads to a special hybrid MDP (with mixed continuous and discrete variables) and poses significant new challenges due to the appearance of an underlying Markov jump parameter governing the mode of the system dynamics. Specifically, the state of a MJLS does not form a Markov chain and hence one cannot study the MJLS control problem as a MDP with solely continuous state variable. However, one can augment the state and the jump parameter to obtain a MDP with a mixed continuous/discrete state space. We discuss how control theory sheds light on the policy parameterization of such hybrid MDPs. Then we modify the widely used natural policy gradient method to directly learn the optimal state feedback control policy for MJLS without identifying either the system dynamics or the transition probability of the switching parameter. We implement the (data-driven) natural policy gradient method on different MJLS examples. Our simulation results suggest that the natural gradient method can efficiently learn the optimal controller for MJLS with unknown dynamics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge