Policy Iteration for Relational MDPs
Paper and Code
Jun 20, 2012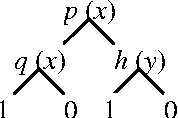
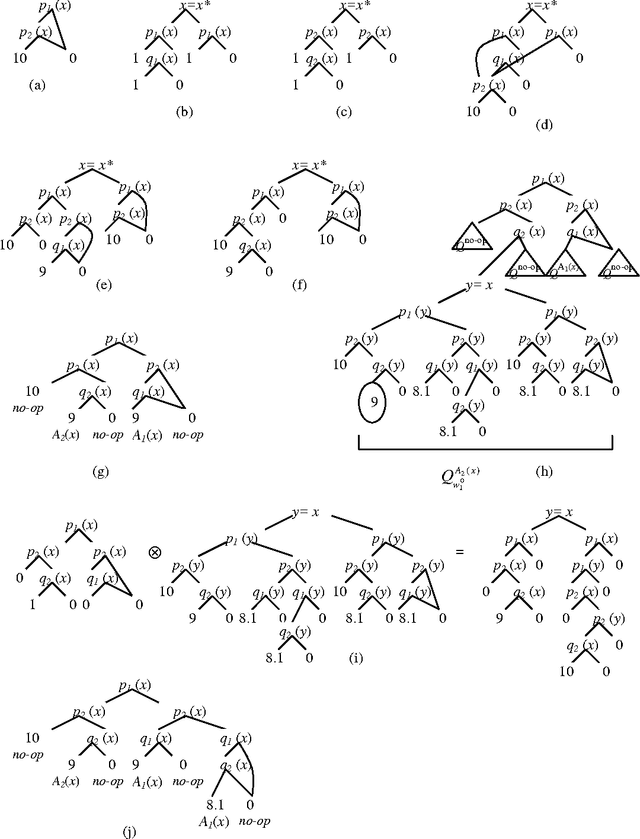
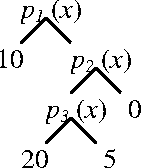
Relational Markov Decision Processes are a useful abstraction for complex reinforcement learning problems and stochastic planning problems. Recent work developed representation schemes and algorithms for planning in such problems using the value iteration algorithm. However, exact versions of more complex algorithms, including policy iteration, have not been developed or analyzed. The paper investigates this potential and makes several contributions. First we observe two anomalies for relational representations showing that the value of some policies is not well defined or cannot be calculated for restricted representation schemes used in the literature. On the other hand, we develop a variant of policy iteration that can get around these anomalies. The algorithm includes an aspect of policy improvement in the process of policy evaluation and thus differs from the original algorithm. We show that despite this difference the algorithm converges to the optimal policy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge