Point cloud denoising based on tensor Tucker decomposition

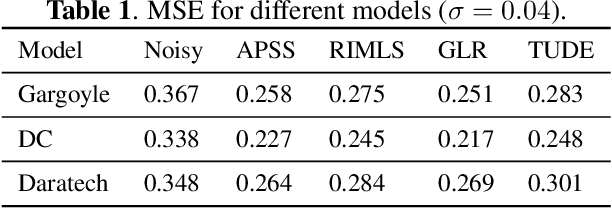
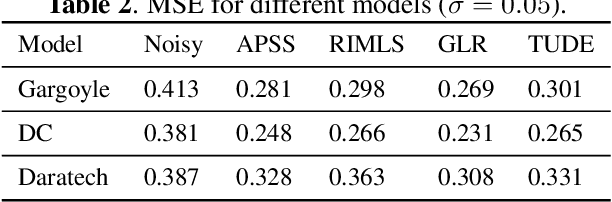
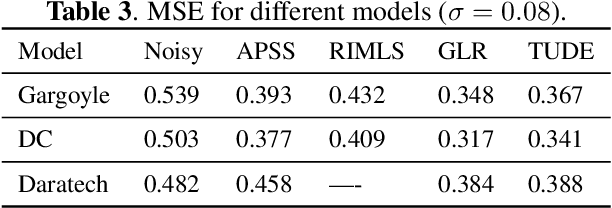
In this paper, we propose an algorithm for point cloud denoising based on the tensor Tucker decomposition. We first represent the local surface patches of a noisy point cloud to be matrices by their distances to a reference point, and stack the similar patch matrices to be a 3rd order tensor. Then we use the Tucker decomposition to compress this patch tensor to be a core tensor of smaller size. We consider this core tensor as the frequency domain and remove the noise by manipulating the hard thresholding. Finally, all the fibers of the denoised patch tensor are placed back, and the average is taken if there are more than one estimators overlapped. The experimental evaluation shows that the proposed algorithm outperforms the state-of-the-art graph Laplacian regularized (GLR) algorithm when the Gaussian noise is high ($\sigma=0.1$), and the GLR algorithm is better in lower noise cases ($\sigma=0.04, 0.05, 0.08$).