Plug-in Channel Estimation with Dithered Quantized Signals in Spatially Non-Stationary Massive MIMO Systems
Paper and Code
Jan 11, 2023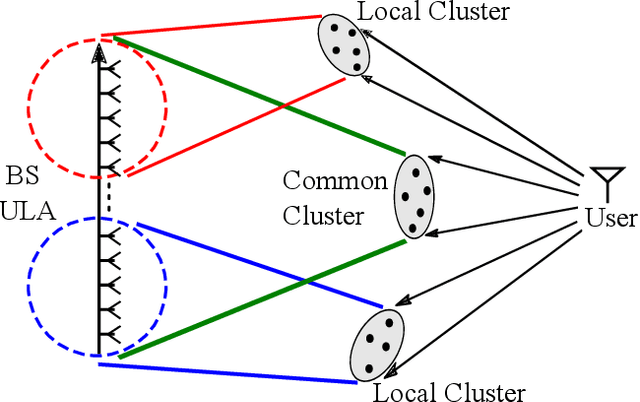
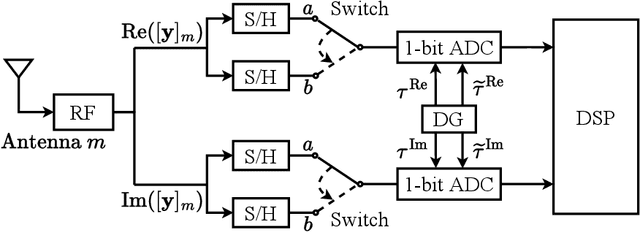
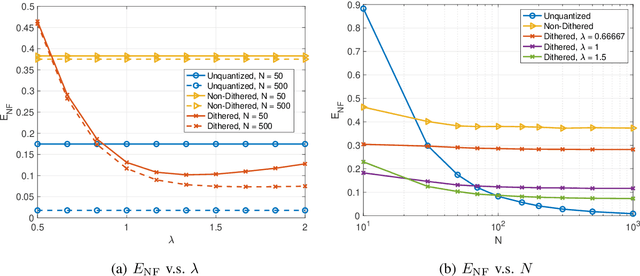
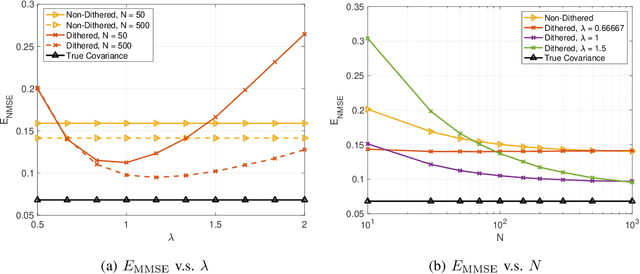
As the array dimension of massive MIMO systems increases to unprecedented levels, two problems occur. First, the spatial stationarity assumption along the antenna elements is no longer valid. Second, the large array size results in an unacceptably high power consumption if high-resolution analog-to-digital converters are used. To address these two challenges, we consider a Bussgang linear minimum mean square error (BLMMSE)-based channel estimator for large scale massive MIMO systems with one-bit quantizers and a spatially non-stationary channel. Whereas other works usually assume that the channel covariance is known at the base station, we consider a plug-in BLMMSE estimator that uses an estimate of the channel covariance and rigorously analyze the distortion produced by using an estimated, rather than the true, covariance. To cope with the spatial non-stationarity, we introduce dithering into the quantized signals and provide a theoretical error analysis. In addition, we propose an angular domain fitting procedure which is based on solving an instance of non-negative least squares. For the multi-user data transmission phase, we further propose a BLMMSE-based receiver to handle one-bit quantized data signals. Our numerical results show that the performance of the proposed BLMMSE channel estimator is very close to the oracle-aided scheme with ideal knowledge of the channel covariance matrix. The BLMMSE receiver outperforms the conventional maximum-ratio-combining and zero-forcing receivers in terms of the resulting ergodic sum rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge