Pitfalls of Gaussians as a noise distribution in NCE
Paper and Code
Oct 01, 2022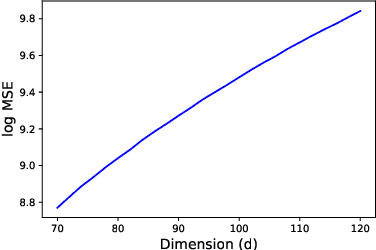
Noise Contrastive Estimation (NCE) is a popular approach for learning probability density functions parameterized up to a constant of proportionality. The main idea is to design a classification problem for distinguishing training data from samples from an easy-to-sample noise distribution $q$, in a manner that avoids having to calculate a partition function. It is well-known that the choice of $q$ can severely impact the computational and statistical efficiency of NCE. In practice, a common choice for $q$ is a Gaussian which matches the mean and covariance of the data. In this paper, we show that such a choice can result in an exponentially bad (in the ambient dimension) conditioning of the Hessian of the loss, even for very simple data distributions. As a consequence, both the statistical and algorithmic complexity for such a choice of $q$ will be problematic in practice, suggesting that more complex noise distributions are essential to the success of NCE.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge