Physics-Integrated Variational Autoencoders for Robust and Interpretable Generative Modeling

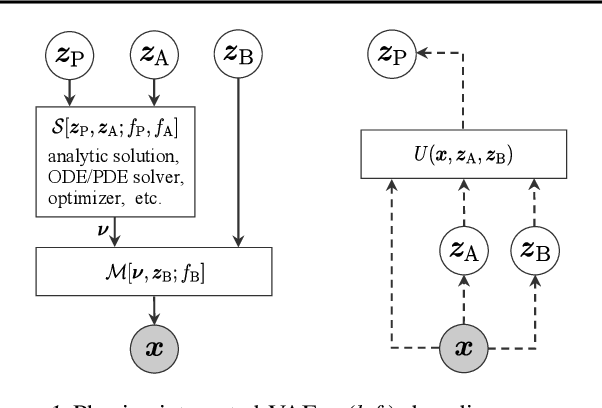
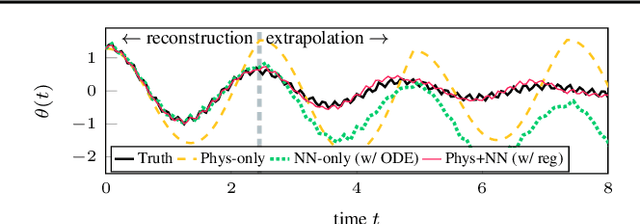
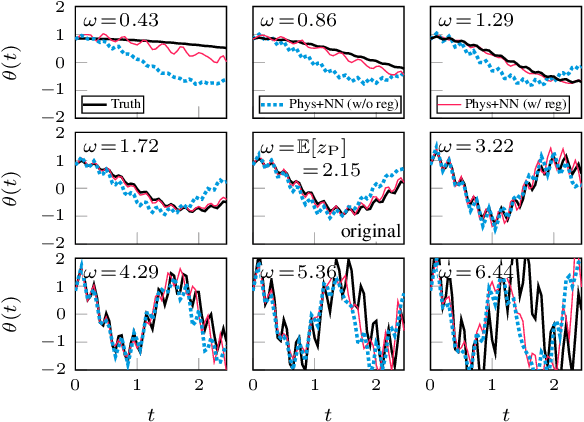
Integrating physics models within machine learning holds considerable promise toward learning robust models with improved interpretability and abilities to extrapolate. In this work, we focus on the integration of incomplete physics models into deep generative models, variational autoencoders (VAEs) in particular. A key technical challenge is to strike a balance between the incomplete physics model and the learned components (i.e., neural nets) of the complete model, in order to ensure that the physics part is used in a meaningful manner. To this end, we propose a VAE architecture in which a part of the latent space is grounded by physics. We couple it with a set of regularizers that control the effect of the learned components and preserve the semantics of the physics-based latent variables as intended. We not only demonstrate generative performance improvements over a set of synthetic and real-world datasets, but we also show that we learn robust models that can consistently extrapolate beyond the training distribution in a meaningful manner. Moreover, we show that we can control the generative process in an interpretable manner.