Physics-informed regularization and structure preservation for learning stable reduced models from data with operator inference
Paper and Code
Jul 06, 2021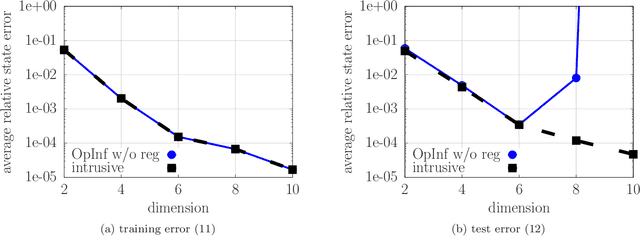
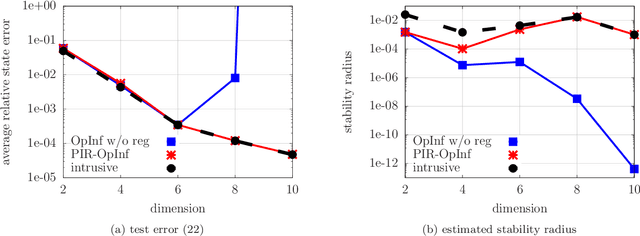
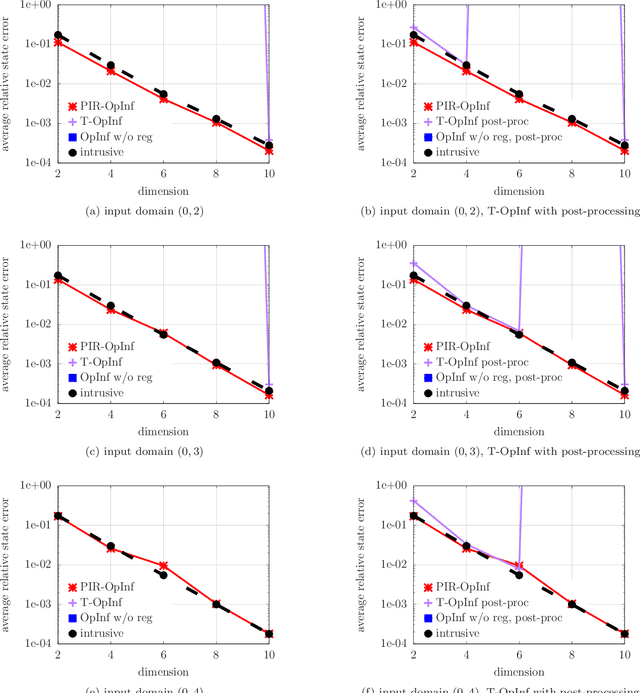
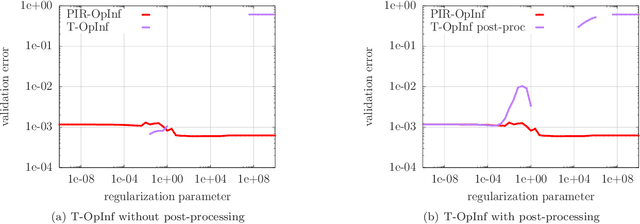
Operator inference learns low-dimensional dynamical-system models with polynomial nonlinear terms from trajectories of high-dimensional physical systems (non-intrusive model reduction). This work focuses on the large class of physical systems that can be well described by models with quadratic nonlinear terms and proposes a regularizer for operator inference that induces a stability bias onto quadratic models. The proposed regularizer is physics informed in the sense that it penalizes quadratic terms with large norms and so explicitly leverages the quadratic model form that is given by the underlying physics. This means that the proposed approach judiciously learns from data and physical insights combined, rather than from either data or physics alone. Additionally, a formulation of operator inference is proposed that enforces model constraints for preserving structure such as symmetry and definiteness in the linear terms. Numerical results demonstrate that models learned with operator inference and the proposed regularizer and structure preservation are accurate and stable even in cases where using no regularization or Tikhonov regularization leads to models that are unstable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge