Permutation Invariant Graph Generation via Score-Based Generative Modeling
Paper and Code
Mar 02, 2020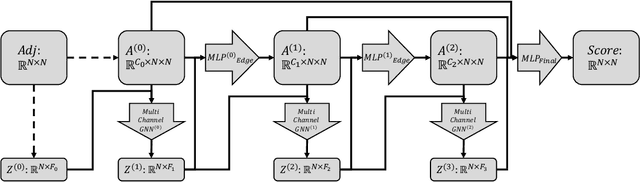

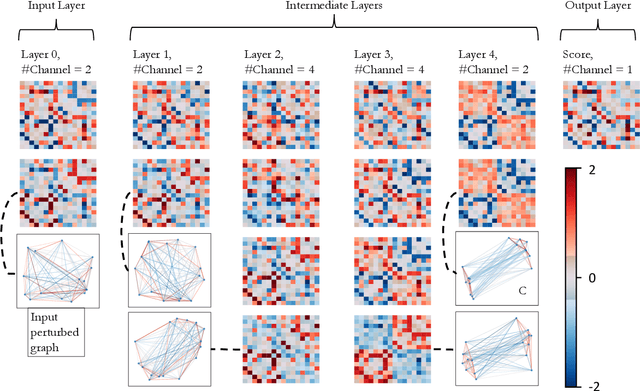
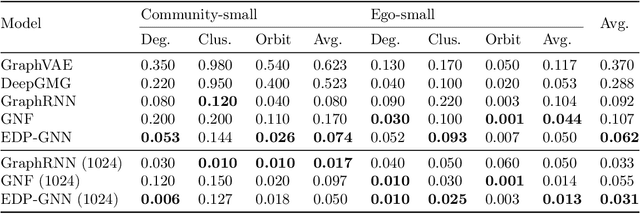
Learning generative models for graph-structured data is challenging because graphs are discrete, combinatorial, and the underlying data distribution is invariant to the ordering of nodes. However, most of the existing generative models for graphs are not invariant to the chosen ordering, which might lead to an undesirable bias in the learned distribution. To address this difficulty, we propose a permutation invariant approach to modeling graphs, using the recent framework of score-based generative modeling. In particular, we design a permutation equivariant, multi-channel graph neural network to model the gradient of the data distribution at the input graph (a.k.a., the score function). This permutation equivariant model of gradients implicitly defines a permutation invariant distribution for graphs. We train this graph neural network with score matching and sample from it with annealed Langevin dynamics. In our experiments, we first demonstrate the capacity of this new architecture in learning discrete graph algorithms. For graph generation, we find that our learning approach achieves better or comparable results to existing models on benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge