Per-sample Prediction Intervals for Extreme Learning Machines
Paper and Code
Dec 19, 2019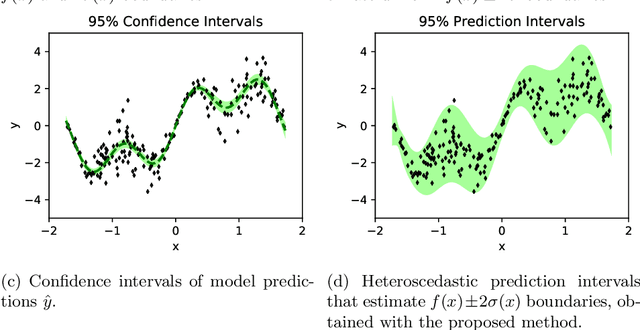

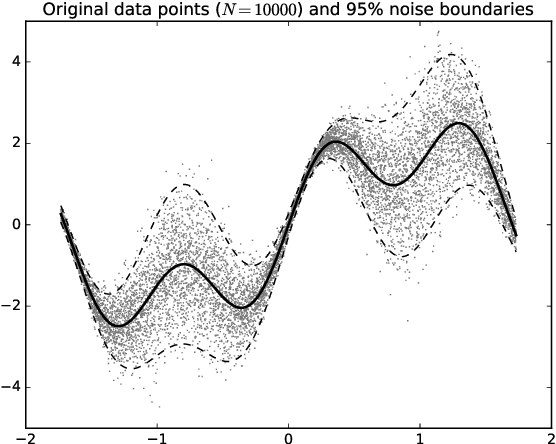

Prediction intervals in supervised Machine Learning bound the region where the true outputs of new samples may fall. They are necessary in the task of separating reliable predictions of a trained model from near random guesses, minimizing the rate of False Positives, and other problem-specific tasks in applied Machine Learning. Many real problems have heteroscedastic stochastic outputs, which explains the need of input-dependent prediction intervals. This paper proposes to estimate the input-dependent prediction intervals by a separate Extreme Learning Machine model, using variance of its predictions as a correction term accounting for the model uncertainty. The variance is estimated from the model's linear output layer with a weighted Jackknife method. The methodology is very fast, robust to heteroscedastic outputs, and handles both extremely large datasets and insufficient amount of training data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge