Penalized versus constrained generalized eigenvalue problems
Paper and Code
May 04, 2015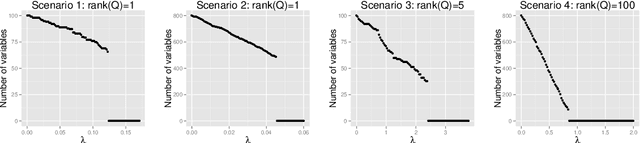
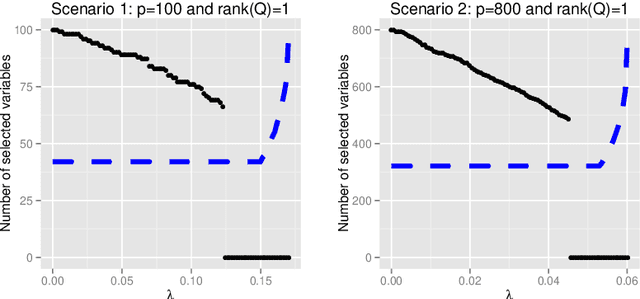
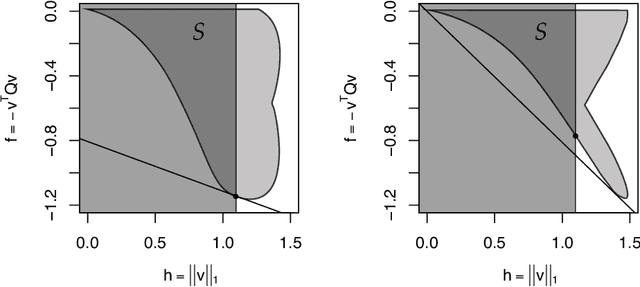
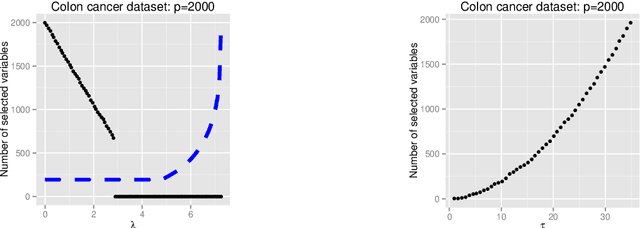
We investigate the difference between using an $\ell_1$ penalty versus an $\ell_1$ constraint in generalized eigenvalue problems, such as principal component analysis and discriminant analysis. Our main finding is that an $\ell_1$ penalty may fail to provide very sparse solutions; a severe disadvantage for variable selection that can be remedied by using an $\ell_1$ constraint. Our claims are supported both by empirical evidence and theoretical analysis. Finally, we illustrate the advantages of an $\ell_1$ constraint in the context of discriminant analysis and principal component analysis.
* 18 pages, 8 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge