Payoff Control in the Iterated Prisoner's Dilemma
Paper and Code
Jul 17, 2018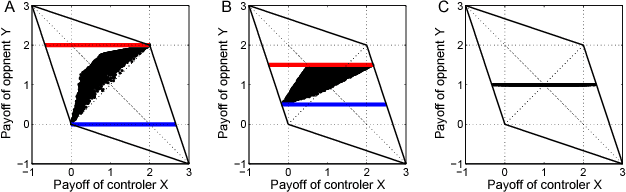
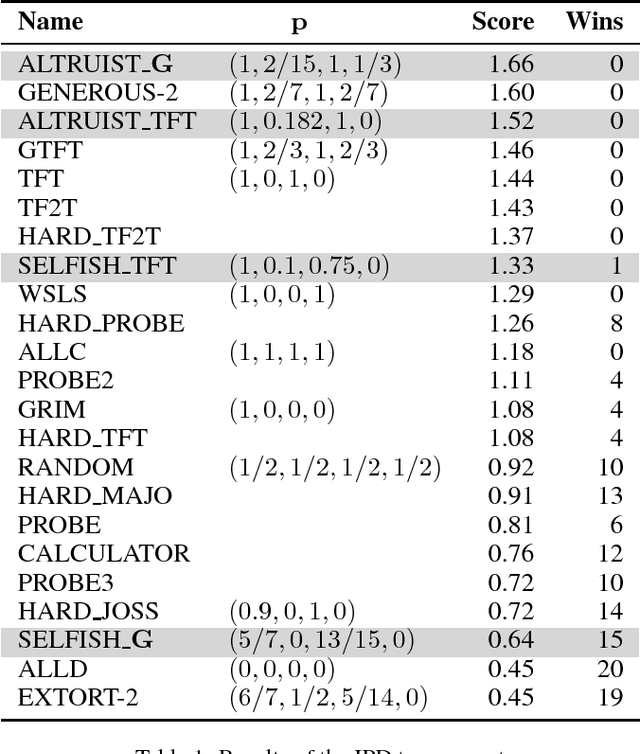


Repeated game has long been the touchstone model for agents' long-run relationships. Previous results suggest that it is particularly difficult for a repeated game player to exert an autocratic control on the payoffs since they are jointly determined by all participants. This work discovers that the scale of a player's capability to unilaterally influence the payoffs may have been much underestimated. Under the conventional iterated prisoner's dilemma, we develop a general framework for controlling the feasible region where the players' payoff pairs lie. A control strategy player is able to confine the payoff pairs in her objective region, as long as this region has feasible linear boundaries. With this framework, many well-known existing strategies can be categorized and various new strategies with nice properties can be further identified. We show that the control strategies perform well either in a tournament or against a human-like opponent.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge